Introduction; Inductors and Capacitors

Inductors and capacitors are one of the basic elements of a resonating circuit. These are circuit elements which have two terminals. The voltage across their terminals is proportional to the passing current through its terminals. The defining property of the any inductor and/or capacitor is its proportionality coefficient. Inductors and capacitors are used to model/define the magnetic field effects on the circuit variables. The stored energy of the magnetic fields has an effect on the current and voltage; therefore inductor-components are used to model these effects.

The relationship of an inductor with the voltage across its terminals and the passing current can be defined as:

                                         (1)

Where V_L= Voltage across the terminals of the inductor

i_L= current through inductor

L_X = Inductance of inductor

The unit H (Henry) is equal to Vs/A (Volt-second per Ampere).

The relationship for a capacitor with the voltage across its terminals and the passing current can be defined as:

                                          (2)

Where V_C= Voltage across terminal of the capacitor

i_C= current through the capacitor

C_X = Capacitance

The unit F (Farad) is equal to As/V (Ampere-second per Volt and F = C/V)

Electromagnetic Waves

Electromagnetic waves can be described by the microwaves by presenting the frequency range of 300 MHz - 300GHz, where the wavelength of the selected waves is 1 m - 1 mm in free space. The electromagnetic waves with the frequency range between 30 GHz 300 GHz are also termed as millimeter waves as in this range the waves have the wavelengths in millimeters which is 1–10 mm. The infrared spectrum can be observed beyond the millimeter wave region. The infrared waves are the electromagnetic waves with wavelength ranges from 1µm to 1mm. another spectrum called visible optical spectrum, ultraviolet spectrum, and x-rays can be seen beyond the level of the infrared region.

The radio frequency spectrum is just below the spectrum of the microwave frequency.  The boundary of the frequency has been observed to be arbitrary for the spectrum between the microwave and radio frequency. However the type of technology used to exploit particular type of the spectrum specify the frequency range. Thus considering the application of the microwaves, radar, communication, sensing, radio astronomy, instrumentation in medical and navigation are the major fields of study which uses the spectrum of the frequency ranges from 300 kHz -300 GHz.  The frequency spectrum has been divided further into other sub frequency bands. Filters are the important devices for producing variety of microwave applications. Different frequencies can be separated and combined by using filters. The limited attributes of the electromagnetic spectrum requires to be shared i.e. filters can be used to confine or select the radio frequency signals within the spectral limits which are already assigned (Hong and Lancaster, 2001).

Other technologies including wireless communication are one of the emerging applications which are found to challenge the microwave filters with their smaller size, lower cost, stringent requirements and higher performances. The designing of the microwave filters is dependent upon the specifications and requirements. The designers may include distributed element and lumped elements. Numerous transmission line structures including coaxial line, micro-strip or waveguide can be considered for the application of the filter design. A rapid development in the field of filter and micro-strips has been found due to the advancements in the technologies of fabrication and novel materials including MEMS (micro-electro-mechanic system), MMIC (monolithic microwave integrated), and LTCC (low-temperature co-fired ceramics) and high-temperature superconductor. The filter design was further revolutionized by the advancements in the tools of the computer aided designs such as simulators of full-wave electromagnetism.

Considering different areas of the microwave engineering the filter systems are the most important building blocks. The signals of different frequencies can be rejected; selected, combined or separated by using these filter systems in host microwave equipment. The variations of the physical realization of such systems can be observed for different frequencies however the topology of the circuit network is same for all (Matthaei et al, 1964).

For the direct measurement of the currents and voltages the ammeters and voltmeters are not available at microwave frequencies. Therefore the current and voltage cannot be taken as the primary measure for the electrical excitations at microwave frequencies. However the operation of the network of microwaves can be described in terms of the filter networks for impedance, currents and voltage measurement which also allow the optimum use of the concepts of the low-frequency network (Hong and Lancaster, 2001)

Microstrip Lines

Structure

The structural visualization of the micro-strip is shown in Figure 1. The top of the dielectric substrate is shown in terms of the conducting strip which has been labeled as W and t as a width and thickness respectively. The bottom of the substrate is shown as a conducting plane which is a ground. The relative dielectric constant is r with relative thickness of h as illustrated in figure 1 below

Waves

There are two media which separates the fields within the micro-strip. These media include air and dielectric above and below respectively to make the structure homogenous.  The pure TEM wave has not been observed to be supported by the micro-strip as it has a homogenous nature. The transverse component of the pure TEM wave can be considered as a basic reason of this non-supportive nature of the micro-strip (Hong and Lancaster, 2001). The material properties including permeability and permittivity dictate its propagation velocity.

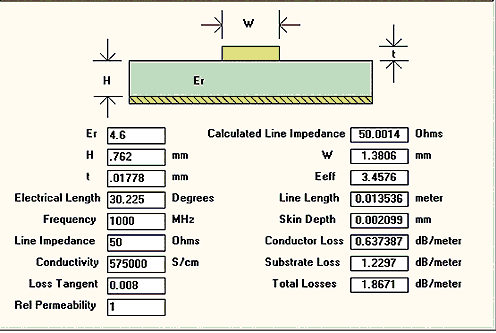
Fig.1: Example Microwave stripline structure

Design of a microwave filter

The design procedure is based on an iterative cycle (Huang and Xiong,2003) where an early design is simulated, the resonant frequencies and the real coupling coefficients found are obtained by curve fitting and associated with their desired values, and then the micro-strip lengths and spacing are adjusted. The iterations meet gradually due to certain estimations.

A microwave filter is a two port network which has low attenuation levels and high attenuations levels in its pass band and stop-band respectively.  In the system of microwave the technology is used to control the frequency response. The characteristics of the frequency responses include high-pass, low-pass and band-pass. Radar, test measurement systems or any communication systems of the microwave systems can be considered as the applications of the microwave filter. The history of the filter theory can be found in the preceding years of the World War II. The main pioneers of the technology are by pioneers such as Mason, Sykes, Darlington, Fano, Lawson and Richards. It was late 1930s when the method of the image parameter was developed for the effective design of the filter. The design was found to be useful in the systems of radio and telephony by using filters of low frequency. Considering the development eras of the coupler and the filter a group including Mathaei, G., Young, L., Jones, E., Cohn, S., and others at Research Institute of Stanford is found to be the most active in the mid of 19^th century. Recent developments in the software that which aid the design of through software modeling have been developed through research and development, such as ‘Ansoft Designer’. These packages use insertion-loss methodology for the simulations

Compact and wide band microwave devices are two of the most recent developments in the field of communication engineering. These developments have the potential to be used in wideband communication systems. Almost all transmitters and receivers use microwave filters as an integral component. However, a microwave filter can only used in wideband applications if it has acceptable wideband frequency response. Planar microwave filters including microstrip filters are the best choice in this regard mainly due to their easy installation, high quality and reliability and small size.

Innovative structures are typically used in an effort to design these kinds of microwave filters. Spiral filters are another type of compact and wideband filters which use single spiral resonators. Although the spiral filters are small in size, they are capable of handling high power, thanks to some of their interesting properties. Furthermore, they offer high Q factor, insensitivity to the fabrication process and high efficient despite using a very small area. According to the literature, there are some spiral filter that offers compact structures (Huang, 2003; Huang & Xiong, 2003).

Filters with quarter wave length spiral resonators with the capacity of a second pass-band were shown by many researchers in including Matthaei et al (1964). It has also been reported that the production of dual band filter with dual spiral resonators and fabrication of a filter with quasi spiral resonators was possible (Huang, 2005). However, in this paper, we will be looking at the fabrication of two kinds of spiral filters that will use microstrip patches rather than a small area at about 1 GHz frequency.

One of the two filters is quasi elliptic filter that has around 11 percent relative bandwidth with nonadjacent coupling and the other one is Chebyshev filter that has around 20 percent relative bandwidth. Both the filters under consideration are micro size at about 500 microns. This small size will be useful and also suitable for physical performance. The ROGERS Corporation in the United Kingdom was contacted to obtain a piece of RT5870 sheet, which is about 1.60 mm thick and offers 2.35 permittivity.

There are a couple of noteworthy advantages attached to utilising patch capacitors. One of these advantages is the fact these capacitors can replace the little gaps between resonators by improving the external and internal coupling. Secondly, with patch capacitors there is no need for the filter structure to have via holes since the quasi quarter wavelength resonators have been used in the filters under consideration. The resonator used is not the same as quarter wavelength resonator since there is a difference between the quarter wavelength with one end short circuited and the boundary conditions of the resonator. The proposed resonators, however, was named as the quasi quarter wavelength resonator as its configuration was mainly based on quarter wavelength.

The quasi elliptic and Chebyshev filters have an area of 6 cm *4 cm and 7 cm * 3 cm and they are relatively compact in the proposed frequency range. Additionally, asymmetric frequency response can be tackled since the quasi elliptic filter uses non identical resonators. This led to having two zero diffusions.

Creation of filter with a wider region free of spurious signals was made possible by using quasi quarter wavelength spiral resonators which do not resonate at twice their centre frequency and are relatively small.  Programmatic network administrator series network analyser from Agilent Technologies in the United States was used to measure the fabricated filters. Findings achieved from the procedure showed similar to the results obtained from the Sonnet Software. Figure 2 shows the two types of aperture couplings typically included in the filter design.

Where,

1. and dy. are the dimensions of aperture on the common ground plane

h is the substrate thickness

g, a and w are the dimensions of the microstrip open loop resonator

The aperture is placed to achieve strongest magnetic field on both sides for the primary resonant mode. Therefore, the aperture can be named as the magnetic aperture and the consequential coupling can be referred to as the magnetic coupling. Similarly, the Figure 3 shows the aperture position at a place where the electric field prevails and hence the resulting aperture can be called the electric aperture and the coupling may be named as the electric coupling.

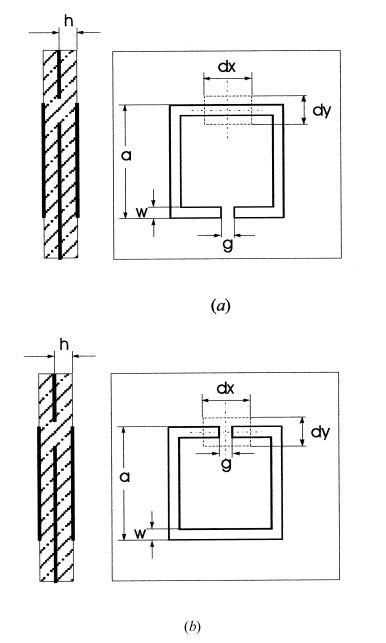
Fig.2: Two micro-strip open-loop resonators, (a) Coupled Magnetically, (b) Coupled Electrically.

The figure 3 shows the structure of resonator band-pass filter that consist on two arrays of micro-strip open-loop resonators located outer side of the two dielectric substrates with a common ground plane in between.

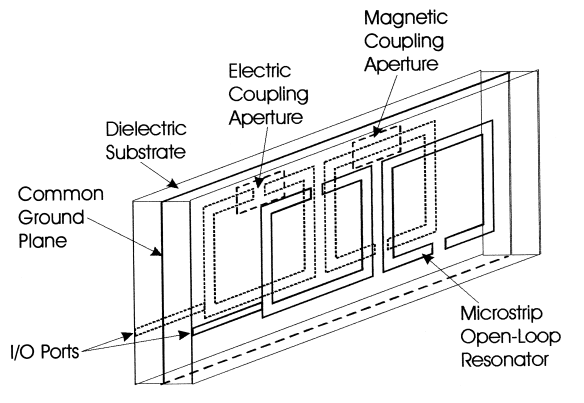
Fig. 3(a): Structure of micro-strip open-loop resonator filter

A full wave Electro Magnetic simulation(s) was completed to understand the characteristics of these two types of aperture couplings (Hong and Lancaster, 1999). Two split resonant-mode frequencies are easily identified by the two resonant peaks. Larger diameter size of the micro-strip-line generates wider separation of the 2 modes and strength full couplings. Independent of the coupling strength and the size of aperture, the low mode frequency of the electric coupling and the high mode frequency of the magnetic coupling remain unaffected. However this scenario is not the same as that indentified in single layer micro-strip coupled resonators in the open loop, in which the resonant frequencies of both modes vary with respect to coupling strength. It was found that this variation is produces because of the effect(s) of coupling-aperture resonant-frequency of uncoupled-resonators. The increase in inductance-resonance was noted to be increased with the aperture orientation at ground-plane. And hence, the resonant frequency of microstrip open-loop resonators is expected to decrease for/against magnetic-aperture or it is expected to increase for/against the electric aperture. Hong and Lancaster in 1999 proved the Electro Magnetic simulated-resonant frequency(s) of the uncoupled resonators in the presence of a coupling-aperture.

 Coupling Coefficient

The design of microwave band-pass filters typically incorporates the coupling coefficients of resonators. Direct synthesis of narrow band filter can be performed using this very accurate technique. Furthermore, optimisation synthesis of wide band filters can also be executed by using the initial structure parameters. It should be noted that the physical properties of resonator filters are wide used as part of the intelligent filter optimization techniques (Cohn, 1957; Hong and Lancaster, 2009).

The frequency dispersion of coupling coefficients results in the asymmetrical slopes of the bassband filters. Attenuation poles, on the other hand, become null mainly due to the coupling coefficients of resonators. The unusual dependence of the coupling coefficients on the distance of some resonators can be explained by energy approach to coupling coefficients (Belyaev et al, 1996). However, the definition of a resonator coupling coefficient is currently not available. In the case of wide band filters (strong coupling), the unusual character of the resonator coupling coefficient is further uncovered.

Resonant Band-pass Networks

The first person who introduced the coupling coefficients into the microwave filter theory was M.Aisal (Hong and Lancaster, 1999). The said researcher started his work from a band pass network which consisted of; alternate and/or parallel resonant circuits (dissipative) which were set to the same frequency of resonance.

The coupling coefficient he defined for this network between adjacent resonant circuits as:

             ,                                                              (3)

Where,

 C_s = Capacitance of the Resistor Inductor Capacitor (RLC) resonant circuit, and C_p = Capacitance of R.L.C resonant circuit (parallel). The Network Transfer Immitance expression is a ratio of the frequency ω, and proportional to the product of coupling-coefficients of every bordering resonant-circuits whereas the denominator is comprised of () with the maximum exponent n; the number of resonant-circuits. Each coefficient in the polynomials is an exclusive function of the coupling-coefficients and the Q-factors of the resonant-circuits. The algebraic expression can be given in the form of Chebyshev polynomial at some values of the coupling-coefficients of the circuits.  The simultaneous equations for those values have been expressed and derived in by Hong and Lancaster in 1999, for the value of n up to or equal to four. So the coupling coefficient k defined by Cohn, 1957 for an unlimited value range.

The ladder-chain of RLC parallel resonant circuits including capacitive and mutual inductive coupling band-pass network was considered. Physical accomplishment/production of such network is much more practical. It has also been expressed that the transfer immitance fraction of the supplementary network is not a polynomial(s) of;

( )

The 2 band-pass networks are more or less equivalent of narrow pass-band filter case, i.e., when ‘|k|’ << ‘1’. Their transfer function coincides in the region of ω₀ if |k| = |k (ω)|, where

                                  (4)

                                          (5)

                   (6)

The C_1., L_1., C_2., L_2.= Inductances, Capacitances of 2 parallel coupled resonant-circuits, and C_m , L_m= Coupling capacitance and mutual inductances. k_L and k_C are inductive and capacitive constants for coupling coefficients of 2 parallel resonant-circuits.

Thus the coupling coefficient k(ω) for 2 parallel RLC resonant-circuits is the sum/addition of two frequency dependent expressions. The first expression is said to be related to capacitive-coupling, where as the second expression represents inductive-coupling. The mathematical sum, given in Eq. (4) may disappear at a specific frequency, given as ω_p, in which transfer-function (of band-pass network) has an attenuation-pole. The phenomenon indicates that inductive-coupling and the capacitive-coupling remunerate each-other. With a resonant-frequency of ω_0, absolute value(s) of both expressions in the mathematical addition (4) are limited to unity.

In research conducted by Bovbysh and Tyunev (2010), it was reported that physical realization of narrow-band filters having no attenuation poles at finite-frequencies should provide the real values for: resonant-frequency (ω₀₎) resonator-factors (Q), and k_i;i+1 which are the coupling-coefficients (b/w resonators). The expression for the coupling coefficient for such scenario can be given as;

                                       (7)

Where ω_e and ω₀ = Frequency (s) of coupled-oscillations of resonators, ω₀ = Resonant-frequency (s), that are for all coupling-reactances. In other words, the coupling coefficient in a narrow passband case is defined as a modeled resonant-frequency constant. However, this simplified approach may not always prove to be successful.

The approximate expression was given by Cohn (1957) as;

                         (8)

Mattaei et al (1964) found the Expression (8) for a bandpass network of coupled non-dissipative microwave resonators. Yet another definition of the coupling coefficient was used therein:

                                  (9)

Where,

i + 1 is an equivalent network of a microwave filter

b_i stands for the susceptance slope parameter for ith resonator

The trait admittance of the inverter between parallel resonators i is given by

Furthermore, it should be noted that at resonant frequency ω_0, all resonators are bound to have 0 susceptance. Equation (10) can be used to determine the slope parameter.

.                                      (10)

The coupled oscillation frequencies ω₀ and ω_e, of 2 similar resonators are mainly responsible for determining the significance of the coupling coefficients at a resonant frequency as shown by approximate formulas (7) and (8). Therefore the coupling coefficient of two identical resonators was expressed by Atia and Williams (1972) as:

                           (11)

For a weak coupling case formula (7) and formula (11) are expected to match. For case of a sole mutual-inductive coupling, it capitulates the |k| value, coinciding with (5) and with (6) in the case of a sole capacitive coupling. In order for formula (11) to be applicable, i.e., equation (6) must suit the given below summarizing regulation for coupling coefficients (Atia and Williams, 1972).

                          (12)

Considering the theory of relativity, formula (12) can be seen as very similar to the velocity-addition equation. For a very weak coupling case, the approximate formula matches with the formula (12) (Ruiz et al, 2008).

                                                 (13)

Values for k, k_L , and k_C can be either negative or positive as assumed by Formulas (11) and (12). The coupling-coefficient sign has meaningful/considerable value when the coupling is compared to another coupling; such as in simulations and modeling.

As for the case of two coupled series and parallel resonant circuits, the frequencies of coupled oscillations ω± are related to the coupling coefficient (3) as follows:

.                          (14)

Solving (14) gives the coupling coefficient

                            (15)

This formula agrees with approximate expression (7). Being equivalent to (3), it may serve as a definition of k.

Using (11) and (15) one is able to compare two different coupling coefficients k and ĸ. They are related as

.                                                (16)

One can see that |ĸ| is greater than |k|. It should be noted that this procedure has never been mentioned in the literature before.

In a bandpass network obtained from a lowpass prototype filter using the bandpass frequency transformation

,                                    (17)

Equation (18) allows us to calculate the frequencies of coupled mode oscillations for resonant circuits.

,            (18)

where Ω is the frequency of the lowpass prototype filter with normalized parameters g_i.

For a bandpass network with alternate series and parallel resonant circuits, using (15) and (18), it is possible to compute the coupling coefficient values.

.                                  (19)

It should be noted that the results obtained from approximate formula k_i,i+1 match with those found from the exact method ĸ_i,i+1.

Coupling Coefficients and Filter Optimization

Various optimization techniques are used in the software packages that are used for microwave modeling.  The smart/intelligent methods for microwave optimization have been proven to be much more useful and effective as compared to the ordinary optimization techniques; because intelligent techniques use the preliminary design information. One such technique was presented by (Belyaev et al 2006), for band-pass microwave filters. The purpose of smart and intelligent optimization technique is to produce the required pass-band and not vary the design parameters much. These parameters are kept constant so that these may use for further optimizations, for example mini-aturization. An objection feature of the intelligence optimization technique is the deflection vector D with n + 1 components.

For n+1 components, n stands for the number of resonators in the filter. The first three components are defined as

                                      (20)

                              (21)

,                        (22)

where ω_c is the current center frequency, ∆ω₀ is the current bandwidth, and R_i is the ith maximum reflected power numbered in the frequency axis direction [5, 6]. Definitions of other components depend on n. In the case of a four-resonator filter,

                                   (23)

,                               (24)

Understanding how to build a proper conjugate correction operation for each deflection components is possible by following certain rules applicable in the intelligence optimization method.

These rules operate in terms of such physical quantities as resonant frequencies of all resonators, external Q factor of input and output resonators, and coupling coefficients for all pairs of adjacent resonators. Components of the deflection vector D are divided into even and odd relative to the center frequency or center reflection maximum(s). Odd components are D₁, D₄. Even components are D₂, D₃, D₅.

Each physical quantity is matched with one the best suitable structure parameter, e.g., the coupling coefficient |k| is matched with spacing S between resonators.

The correction operation for an odd component involves correction operations for frequency-related structure parameters. The correction operation for an even component involves correction operations for coupling-related structural parameters. For example, the correction operation for D₅ > 0 comes down to increasing the coupling coefficient |k₁₂| and simultaneously decreasing the coupling coefficient |k₂₃|; to assure that the value of the product is not changed i.e. |k12|²|k₂₃| (Belyaev et al, 1996).

All correction operations associated with deflection vector apparatus/components are quasi orthogonal, which specifies that every correction operation, with elimination of conjugate-deflection-component, produces other deflection-components having the absolute-value lower than the absolute-value of initial deflection-component.

Computation and examination of strip and microstrip filter and analysis and synthesis have been successfully performed over the last ten years using the intelligence optimisation techniques (Belyaev et al, 2007). The intelligence optimisation method has recently become a widely used method for bandpass filters with dual mode resonators.  Instead of using one oscillation ode per resonators, the pass band formation in these filters incorporates two vibration modes. It is recommended to treat each dual mode filter resonator as a pair of couple single mode resonators for the rules formulated for single mode filter to be applicable. The two resonant frequencies of the actual dual mode resonator, therefore, must match with the frequencies of coupled vibration in such an imaginary setting. A simulation or experiment can be performed to obtain an answer to how to control the coupling coefficient and resonant frequencies of coupled imaginary resonators.

Another area of application of coupling coefficients for filter optimization has to do with the coupling matrix (Li et al, 2008) and the extended coupling matrix, which are even. Coupling coefficients kij between jth and ith resonators are the off diagonal elements of these matrices. Cross coupling between non adjoining resonators can therefore be achieved. It is assumed that the coupling coefficients in these matrices are not dependent on frequency. Furthermore, using the extended coupling matrix and the coupling matrix, it is possible to calculate the frequency response of an equivalent network. Space mapping optimisation of coupled resonator microwave filters is also based on these common models (Amari et al, 2006).

A similarity transformation for the extended coupling matrix can be completed as we move to linear combination from resonator voltages. The overall frequency response is not affected by these transformations though and therefore it will not be wrong to say that all these transformations are alike. Once of these transformed matrices is known as the transversal matrix which results in all off diagonal elements to be zero. On the other hand, the diagonal elements of the coupling matrix are taken as the Eigen values. Additionally, it should be noted that the Eigen modes are not attached to each other. Amari and Bekheit (2007) thoroughly discuss the similarity transformations and the physical understanding of this concept.

Conclusion

The design of spiral microstrip filters is present in this report.  Chebyshev and quasi-elliptic filters were considered for this design. For both the frames, external and internal couplings were explained, including the diagrams, and calculation were carried out to find out the fitting structure.  Addition of the microstrip patches capacitor in-between the resonators showed increase in the coupling. Furthermore, external coupling also increased through the utilization of the capacitor. Additionally, by using a patch capacitor, the use of using via holes was avoided in the filter structure. It was seen that quasi quarter-wavelength resonator filters had the advantage of not resonating at a frequency twice as high as that of the main resonance. Furthermore, it was inferred that equality of the resonant frequency of the resonators may lead to an asymmetric response in a filter with nonadjacent coupling; by using non-identical resonators (but retaining the symmetry), two transmission zeroes were set in both sides of the filter response. Thus, two spiral filters were designed, simulated, and fabricated—one Chebyshev filter and one quasi-elliptic filter, whose measured results had very good agreement with simulated results. The fabricated Chebyshev filter had 20% bandwidth, and the fabricated quasi-elliptic filter had 12% bandwidth around 1 GHz. Thus, it can be seen that the quasi quarter-wavelength spiral resonators method for microwave filter design leads to very good results in practical applications.

References

Amari, S., LeDrew, C. and Menzel, W., 2006. Space-mapping optimization of coupled- resonator microwave filters. IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 5, 2153-2159.

Amari, S. and Bekheit, M., 2007. Physical interpretation and implications of similarity transformations in coupled resonator filter design. IEEE Transactions on Microwave Theory and Techniques, Vol. 55, No. 6, 1139-1153.

Atia, A. E. and Williams, A. E., 1972. Narrow-band waveguide filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 20, No. 4, 258-265.

Awai, I., 2006. Meaning of resonator’s coupling coefficient in band-pass filter design. Electron Communication, Japan, Part 2, pp.1–7.

Belyaev, B. A., Kazakov, A. V., Nikitina, M. I.  and Tyurnev, V. V., 1996.  Physical Aspects of Optimal Tuning of Microstrip Filters, Kirensky Institute of Physics.

Belyaev, B. A. and Tyurnev, V. V., 2006. The method for microstrip filters parametric synthesis, Microwave &Telecommunication Technology, pp.17-19.

Belyaev, B. A. and Tyurnev, V. V., 1992. Frequency-dependent coupling coefficients of microstrip resonators. Elektronnayatekhnika. Ser. SVCh-Tekhnika, No. 4, 24.

Cameron, R., 2003. Advanced coupling matrix synthesis techniques for microwave filters. IEEE Transactions on Microwave Theory and Techniques, Vol. 51, No. 1, 1-10.

Cohn, S.B., 1957. Direct-coupled-resonator filter. IRE, Vol. 45, pp.187-196

Dovbysh, I. A. and Tyurnev, V. V., 2010. Synthesis and investigation of three-section microstrip filter on folded dual-mode stepped-impedance resonators," Progress In Electromagnetics Research M, Vol. 12, pp.17-28

Dovbysh, I. A. and Tyurnev, V. V., 2009. Peculiarities of intelligence optimization of a microstrip filter on folded dual-mode resonators, PIERS 2009 in Moscow Proceedings,

Gashinova, M. S., Goubina, M. N., Zhang, G., Kolmakov Y. A., Kolmakov, I. A. and Vendik, I. B., 2003. High-Tc superconducting planar filter with pseudo--Chebyshev characteristic. IEEE Trans, Theory Technol, pp.792–795.

Hong, J. S. and Lancaster, M. J., 1996. Couplings of microstrip square open loop resonators for cross-coupled planar microwave filters. IEEE Trans. Microw. Theory Technol, pp.34-77

Hong, J.S. and Lancaster, M. J., 2001. Microstrip filters for RF/microwave applications, chap. 3. New York: John Wiley & Sons, Inc.

Hong, J.S. and Lancaster, M. J., 2001. Microstrip Filters for RF/Microwave Applications, John Wiley & Sons, New York.

Hong, J.S. and Lancaster, M. J., 1999. Aperture-coupled microstrip open-loop resonators and their applications to the design of novel microstrip bandpass filters, IEEE Trans., MTT-47, Sept.

Huang, F., 2003. Ultra-compact superconducting narrow-band filters using single- and twin spiral resonators. IEEE Trans. Microw. Theory Technol, pp.487–491.

Huang, F. and Xiong, X., 2003. Very compact spiral resonator implementation of narrow-band superconducting quasi-ellipticfilters. InProc. 33rd Eur. Microw, Germany, pp. 1059–1062.

Matthaei, G. L., Young, L.  and Jones, E. M. T., 1964. Microwave Filters, Impedance-matching Networks, and Coupling Structures, McGraw-Hill, New York.

Ruiz, J. A., Wang, C. and Zaki, K. A., 2008. Advances in microwave filter design techniques, Microwave J., Vol. 51, pp.26-42

Li, G., Dai, X. W.  and Liang C. H., 2008. Fast synthesis of coupled-resonator filters.  Journal of Electromagnetic Waves and Applications, Vol. 22, pp.5-6,