Anchor Retaining Walls Deep for Many Floors

Introduction

For highway projects, the anchor retaining walls are designed for the stabilization of the slopes and excavations. The anchored walls include non-gravity cantilever walls with different levels of ground anchors.

Need Help with Assignment/Dissertation Writing? Get A Response within 24 Hours!

The anchor retaining walls are found to employ the continuous or discrete vertical elements which can be drilled to the depths below the grades of excavations which are finished previously. Support in such anchored walls is usually provided by the bending and shear stiffness of the elements of the vertical walls and resistances offered by the soils lying below the grades of excavation.

These components are required to support the anchored walls, ground anchors are used to providing the lateral resistance which can be used for resisting the horizontal pressures applied to the wall i.e. earth, water, seismic, etc. There are numerous methods used to design the wall elements of the anchored walls.

The drilled shafts or steel piles usually form the discrete vertical elements of the anchored walls which can be spanned by using structural facing phenomenon.  The construction of depressed roadways, roadway alignments and widening of roads requires the grade separation that can be done by using anchored walls.

The anchored walls are found to be advantageous when compared with the conventional gravity walls of concrete. The anchored walls are cheaper than the conventional gravity walls as they don’t require excavation support, deep foundation support possibly and selection of a backfill. The anchored retaining walls can also be used for the abutment of the construction of the new bridge and the removal of the abutments of the existing bridge (FHWA-RD-97-130, 1998).

Basic principles of anchored system design

General design concepts for anchor retaining walls

The creation of a stable and internal mass of soil that can be used for resisting numerous modes of structural failures at a certain level of serviceability is called the system of anchor retaining walls. The anchor retaining walls can be designed by considering all potential failures and other conditions. The movements of the soil and that of the wall should be limited during the provision of the economical and practical basis for construction (Abramson, 1993).

The resistance for the mobilization of wall elements and anchors should be considered while designing them to respond to the loads applied to the system of walls. The total force of the anchored walls is required to have a magnitude by maintaining the wall equilibrium which in turn is dependent on the forces caused by the external loads, water and soils.

The stabilized forces can be provided by the anchors and transmitted into the soils through a suitable distance as illustrated in figure a. the minimum distance behind the wall can be estimated by the transmission of the anchor forces behind the active zone, the minimum distance would define the bond length of the anchor formed.

The bond length must be extended to intersect with any potential surfaces of failure which may pass to the anchors and below the wall base as shown in figure b. The depth for the installation of the anchors can be determined by estimating the location of the deepest surfaces subjected to failure. These surfaces usually have insufficient safety factors without the interference of anchor forces.

The soil which is adjacent to the equilibrium excavation should be supported by the anchored walls. The provided support will govern the maximum force required by the anchors and maximum bending moments, strengths and dimensions within the section of the wall. A sufficient extension should be given to the anchors deep into the soil so that the range of the deep-seated and shallow potential surfaces of failure would have sufficient safety factors. The potential slip surfaces are acted upon by the anchor forces and have ensured that they have the safety factors which are more acceptable (American, 1994).

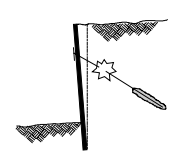
Figure 1: tensile failure of the tendon

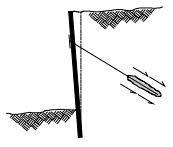
Figure 2: pullout failure of grout

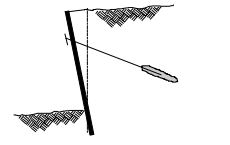
Figure 3: Pullout failure of the tendon

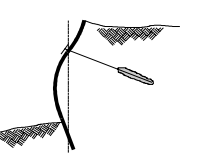
Figure 4: Failure of the wall in bending

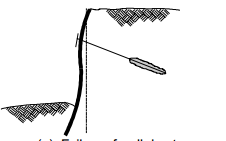
Figure 5: Failure of the wall due to insufficient passive capacity

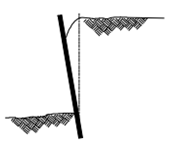
Figure 6:  Failure by forwarding rotation (cantilever before the first anchor installed)

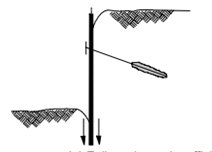
Figure 7: Failure due to insufficient

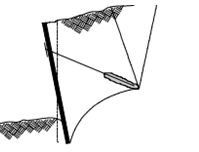
Figure 8: Failure by overturning

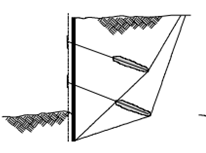
Figure 9: Failure by sliding

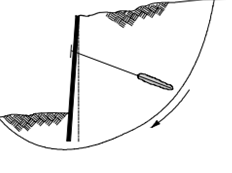
Figure 10: Rotational failure of groundmass

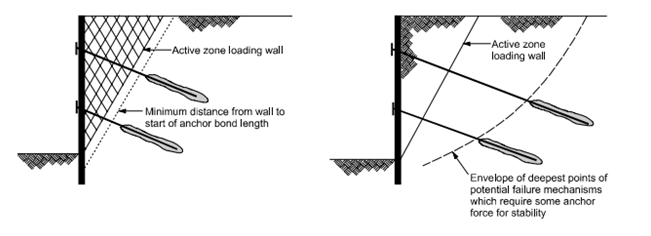
Figure 11: Contribution of ground anchors to wall stability.

Need Help with Assignment/Dissertation Writing? Get A Response within 24 Hours!

Selection of soil parameters for design

Soils can be selected for the efficient design of the anchor retaining walls based on the shear strength forces they have.

Drained Shear Strength of Granular Soils

Granular soils can be represented by the drained shear strengths and the resultant stress friction angles. Deposit is found to be difficult in this case because of the sampling of the granular soil. For designing a wall, the friction angle can be used by accurate estimation procedures.

Undrained Shear Strength of Normally Consolidated Clay

Under undrained conditions, the consolidated clay is found to develop instability under the conditions of the contractive shear for example the deformation mechanisms for the mobilization of the resistances caused by frictional shearing. Under such conditions, the soil also prefers to contract for the confining stresses.

The phenomenon of contracting under the stresses is a typical attribute of the medium and soft clays which are lightly over-consolidated (Andersen, 1984). The permeability of the clay soil concerning the rate of shearing doesn’t let the researcher realize the contracting ability of the soil.

The effective stress of the soil along with the frictional shear resistances are found to be reduced due to the generation of the positive pore-water pressures. In such circumstances, the shearing resistance within the soil is lesser than the conditions under drainage i.e. soil volume contraction.  The short term condition of drainage is considered to be critical for the anchored walls which are constructed in the clay soils with normal to light consolidation.

Undrained Shear Strength of Overconsolidated Clay

When the clay soil is subjected to the conditions of unloading that has been resulted from the excavation process for the formation of the anchored wall, the soil is expanded under the effect of the frictional shearing resistance.  This condition would cause a negative pressure of pore-water which will increase the mobilized frictional shearing resistance and effective stresses within the soils (Barley, 1997).

Thus when the over-consolidated clay is subjected to the excavation, the strength and short term stability would be exceeded after a one-time occurrence of drainage. Stiff to hard over-consolidated soils and clays are preferred for the construction of the temporary and permanent anchored walls. Over-consolidated clay soils which are heavily operated are more subjected to fissure.

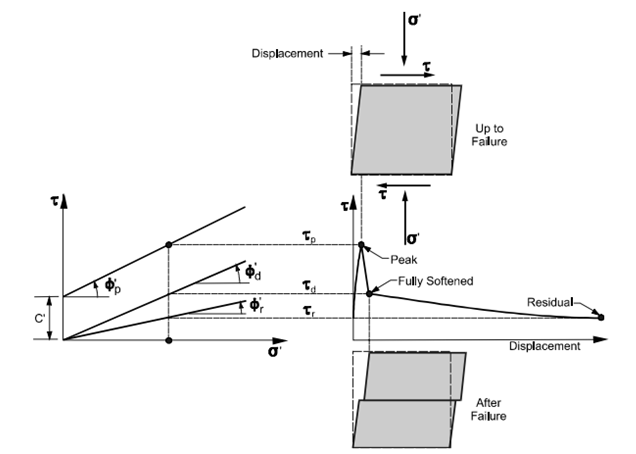
Figure 12: Simplified drained stress-displacement relationship for a stiff clay (modified after Construction Industry Research and Information Association (CIRIA), 1984).

For the over-consolidated clays with stiff hard attributes, the designers of the anchored systems are required to decide the strength which has to be used for the design.  Anchored systems should b designed by using residual strengths for the locations with the evidence of the surface failures that occurred within the clay. The active landslides can be stabilized by the anchored systems.

For such conditions, a sufficiently large deformation can be assumed for the reduction of the strength to a typical residual value. A correlation has been presented by Stark and Eid (1994) for the determination of the relationship between liquid limits, clay fraction size and the angle of residual fraction for the clay soils.

Design of anchored systems                                             

A 13 step procedure is discussed in this chapter for the general illustration of the designing of the anchored systems. The anchored retaining wall has been assumed to be applied for a specific support system. For the selection of a particular wall type FHWA-SA-96-038 (FHWA, 1997) was consulted.

Overall geometric requirements for the system of the anchor retaining walls are established in the first step along with the identification of the project constraints and requirements. The wall profile has been developed in this step. The appurtenances of the wall are located which include utilities, traffic barriers, and requirements of the construction sequences and cost of the wall systems.

Specific structural and geotechnical aspects of designing an anchor retaining wall are addressed from steps 2 to 13. Typically the design steps are illustrated in the following steps (modified after FHWA-RD-81-150, 1982).

Step 1

Basic project requirements are established in this step including external loading, geometry, construction constraints and performance criteria.  

Step 2

The relevant properties of the rocks and soil are evaluated with the assessment of the subsurface conditions.

Step 3

The numerous levels of corrosion protection are selected with the establishment of the design safety factors and design properties.

Step 4

Selection of the earth pressures on the back of the wall for the evaluation of the final wall height. Evaluate total pressure after adding appropriate water and surcharging. If marginal soils are used as a staged analysis of construction will also be required.

Step 5

Wall bending moments and loads of the horizontal ground anchors are calculated in this step. The locations of the vertical anchors will be adjusted for the achievement of the even distribution of the wall bending moment.

Step 6

Considering the right of way limitations, the required anchor inclination will be evaluated. The locations of the underground structures and appropriate anchoring strata are defined.

Step 7

Each load of the horizontal anchor will be resolved into the vertical components of the force and the force applied along the length of the anchor.

Step 8

Based on the different types of walls, the horizontal spacing of anchors will be evaluated. The individual anchor loads are calculated.

Step 9

The type of ground anchor will be selected.

Step 10

The lateral and vertical capacity of the wall below the sub-grade excavation is evaluated. The wall section can be revised if required

Step 11

The internal and external stability of the anchor wall will be evaluated. The geometry of the ground anchor can be revised if required.

Step 12

The maximum wall movements will be estimated along with the surface settlements of the ground.

Step 13

The connection devices, wallers, drainage systems are designed and lagging is selected (Bruce, 1997).

Evaluation of earth pressures for wall design

The distribution of the earth pressure developed on the anchored walls is found to be dependent on the distribution of the deformations of the lateral wall and its magnitude. Sufficiently large deformations are expected in a cantilever wall that is more flexible under non-gravitational modes which are enough to induce the active earth pressure in the entire height of the wall. For designing such systems, theoretical diagrams of the active earth pressures can be used that are developed by using coulomb analysis or Rankine methods.

The deformation patterns are found to be more complex for the anchored wall systems constructed from the system of top-down. Such systems are not consistent to be used with the theoretical design calculations based on the coulomb earth method or Rankine systems of pressure distributions. The deformation patterns of the wall are directly influenced by the anchor inclination, Soil shear strength, vertical spacing of the Anchors, anchor lock-off loads and wall stiffness (Bruen, 1996).

Staged analysis for the construction is required in some circumstances including

• Nearby foundations loading influences the wall
• Wall will be resisted by the large surcharge loadings.
• The retained soil has the preexisting planes or instabilities of weaknesses

The total required load for the stabilization of the excavation or a slope can be evaluated by using limit equilibrium calculations. Hand calculation methods can be performed by conducting limit equilibrium calculations including slope stability analysis through computer programs and trial wedge techniques. The validity of the limit equilibrium calculations is the same as that of the earth pressure diagrams (CIRIA, 1980).

Terzaghi and Peck Apparent Earth Pressure Diagrams

The earth pressure diagrams are illustrated in the figure in which the maximum pressure is denoted by p. following factors is considered while developing the envelopes of the Terzaghi and Peck:

It has been assumed that the excavation is wide and more than 6 m deep. Mobilization of the full value of the soil shear strength can be achieved by assuming the larger wall movements.

For the excavation of sands, the groundwater is assumed to be below the level of the base. However the position is not found to be important in the case of clays i.e.  Water pressure loading will not be considered specifically (FHWA, 1986).

The behaviour and mass of the soil are assumed to be homogenous and drained for sands during shearing. For clays, it has been assumed to be undrained (short term loadings).

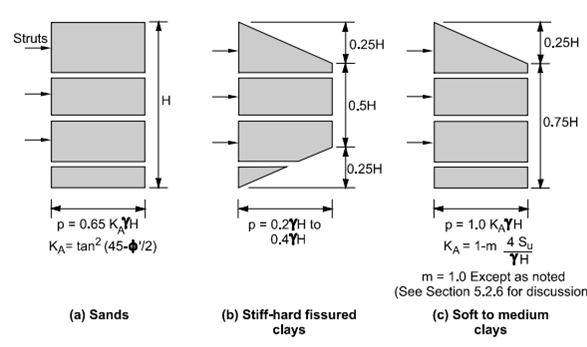
Figure 13: Terzaghi and Peck apparent pressure envelopes (after Terzaghi and Peck, 1967, Soil Mechanics in Engineering Practice, Reprinted by permission of John Wiley & Sons, Inc.).

The exposed portion of the wall will be subjected to the loading diagrams.

The stability numbers are related to the apparent earth pressures for clays and are defined as below:

Where

 γ = total unit weight of the clay soil,

Su = average undrained shear strength of the clay soil below the base of the excavation, a

H = excavation depth. 

Standard SI units are:

γ= (kN/m³),

Su = (kPa),

H = (m). 

Two apparent envelopes of the earth pressure can be developed with high and low Ns values as shown in the figure. The envelopes showed the results for the stiff to hard clays and soft to medium clays. Recommendations for the anchor retaining wall systems are derived by using these diagrams as references.

For sand, the value of Ka can be evaluated as shown in figure a.

The maximum ordinate of the earth pressure is found to be

Where

φ′ =the effective stress friction angle of the sand.

 The total load of the lateral earth has been calculated by using the value of lateral earth pressure from the rectangular apparent earth pressure diagram as shown in figure a for sands. The value is found to be

0.65 KaγH²

The apparent earth pressure envelop for the single level anchored walls or the anchored walls with greater levels of the ground anchors has been recommended to be trapezoidal as shown in figure

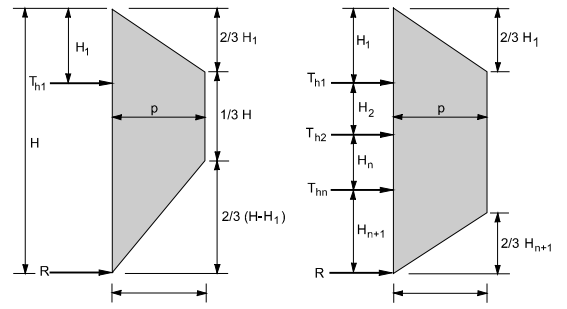
Figure 14:  walls with one level and multi-levels of anchor retaining walls

H1 = distance from the ground surface to the uppermost ground anchor

Hn+1  = distance from the excavation base to the lowermost ground anchor

Thi = horizontal load in-ground anchors

R = reaction force is to be resisted by subgrade

P = maximum ordinate of the diagram

The trapezoidal diagram recommends the location of the lower and upper ends of the ground anchors which are required to construct the apparent diagrams of the earth pressures.  There are many reasons which prove the appropriateness of the trapezoidal diagrams more than the rectangular ones.

• The anchor locations resulting from the arching are found to be concentrated by the earth pressures
• At the ground surface, the earth pressure is zero and found to be more appropriate for sands when no loading of surcharge is present
• Moving from the ground surface to the upper location of the ground anchor, the earth pressures are found to be increased

For sands, the diagram is appropriate to be used for both the short term and long term loadings. The total lateral load acting on the wall is then be calculated by adding the surcharge pressures and water pressures explicitly to the earth pressure diagram (Golder, et.al. 1970).

Recommended Apparent Earth Pressure Diagram for Stiff to Hard Fissured Clays

Temporary Conditions

For the stiff, to hard fissure clays, the apparent earth pressure diagrams have been used in this study. The previous successful experiences of excavation constructions within similar soils are considered for the designing of the anchor retaining walls. The degree of fissuring in the clay is influenced by the earth pressures in the soils (Hanna, 1982).

Observations

One of the most important observations is that the system must resist as much load as twice designed by using an envelope based on the upper range value of the maximum ordinate pressure.

6‑1 summary of trapezoidal apparent pressure envelopes for stiff to hard clays

For the earth pressure diagrams of the Terzaghi and Peck for the temporary loadings, the maximum pressure p has been found to range from 0.2γH - 0.4γH as illustrated in figure b. The total load is thus ranging from 0.15γH²-0.30γH². As the weight of the stiff to hard clay was assumed to be 20 kN/m³. The total load has been estimated through this diagram which is about 3H² - 6H².

Where H has been measured in meters and the total load was measured in kN/m.  The measurement of the ground anchor load was presented by Ulrich (1989) for seven excavation walls. Each of the excavations showed that the stability number Ns is lesser than 4.

Figure 25 showed the measured loads. The maximum ordinate for the earth pressure ranges from 0.1γH- 0.25γH approximately. The ordinates of these maximum pressures illustrate the total load used by Terzaghi and Peck diagram by 1.5H²-3.75H². The apparent earth pressure was found and the value was 0.25γH- 0.35γH. 

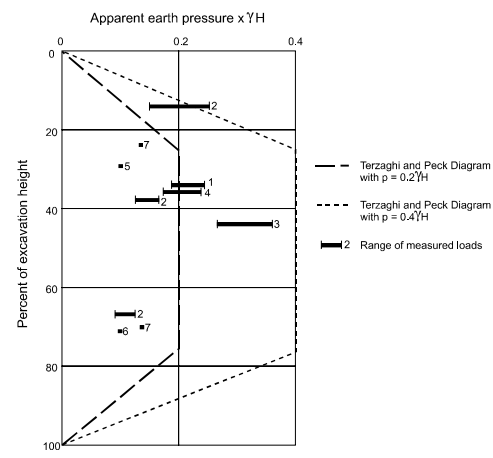
Figure 15: Measured anchor loads for seven projects (after Ulrich, 1989, “Tieback Supported Cuts in Overconsolidated Soils”, Journal of Geotechnical Engineering, Vol. 115, No. 4, Reprinted by permission of ASCE).

The recorded loads and the design pressure envelopes are illustrated in figure 26 in terms of the percentage of the design values. The maximum pressure ordinate of the design pressure envelop has been observed to be equal to 30H psf where H has been measured in feet.

For two test sections, the actual pressure envelops are found to be equal to the 19H psf and 22H psf which is about 65 to 75% of the actual design values. The total load for the design pressure of the 30H the total load is found to be equal to the 24H² lb/ft. For the actual pressure envelops of 19H and 22H, the total load will be 15.2H²-17.6H² lb/ft respectively.

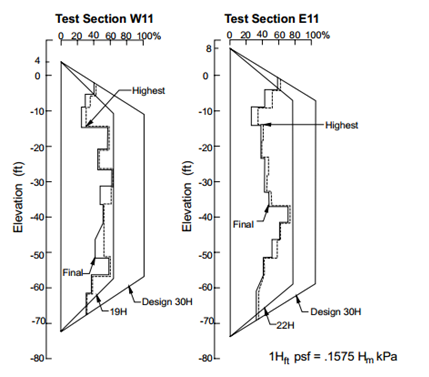
Figure 16: Wall pressure envelopes (after Winter, 1990, “Pacific First Center-Performance of the Tieback Shoring Wall”, Design and Performance of Earth Retaining Structures, Geotechnical Special Publication No. 25, Reprinted by permission of ASCE).

The results have illustrated that from the apparent envelops of the earth pressure by using the maximum values of the pressure ordinate the lower bound values can be represented for the Terzaghi and Peck envelope. The maximum ordinate pressure has to be consistent with the value of total load illustrated from the diagram which is 3H²-6H² approximately.

For stiff t hard clays the apparent diagrams of the earth pressure for the controlled short durations in the absence of the free water. For long term or permanent conditions, these diagrams can be used for the evaluation of the drained strength parameters of the soil. For stiff to hard clays the permanent conditions are described in the following section (Institution 1997).

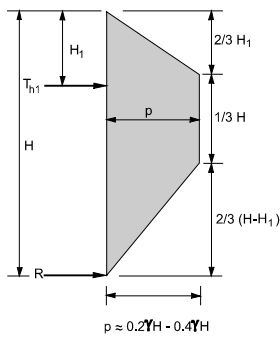
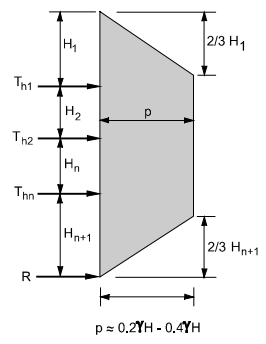
Figure 17: walls with multiple levels of ground anchors                  Figure 18: walls with one level of ground anchors

H1 = distance from the ground surface to the uppermost ground anchor

Hn+1  = distance from the excavation base to the lowermost ground anchor

Thi = horizontal load in-ground anchors

R = reaction force is to be resisted by subgrade

P = maximum ordinate of the diagram

Permanent Condition

For stiff to hard fissured clays the earth pressure diagrams were developed by using original Terzaghi and Peck for temporary loading conditions. For designing permanent walls the earth pressure diagrams associated with temporary conditions are difficult to use (Littlejohn, 1992; Ludwig and Weatherby, 1989).

The diagrams of temporary conditions were used for the calculation of the total resultant force. The values are then compared to results obtained in the recommended earth pressure envelopes by using the total resultant force of about 0.65KAγH². The drained friction angle of the clay soil is found to be dependent upon the value of KA.

The angle of drained friction in most of the applications of the anchored walls is found to correspond to the fully softened friction angle.  The largest value of the resultant force was used from the given diagrams. In an equivalent total force, a drained friction angle of about 39° was resulted after using the maximum pressure ordinate of about 0.2γH.

Recommended Apparent Earth Pressure Diagram for Soft to Medium Clays

Soft to medium clays can be taken to construct the temporary and permanent anchor retaining walls. For the formation of the anchor bond zone, the competent layer is required to be within a reasonable depth below the level of excavation. Where the soft clays extend to the base of excavation the use of permanently anchored walls is not recommended. For the deeper excavations and soft to medium clays the diagrams of the Terzaghi and Peck diagram has been used as shown in figure23c. The coefficient of the total stress earth pressure can be illustrated as follows:

Where

m = empirical factor accounts for potential base instability effects in deeper excavations for the soft clays. 

m is usually estimated to be equal to the 0.4 for the Ns values of more than 6 and the excavation is underlain through deep soft clay. In other situations, m is estimated at 1 (Peck, 1969). The soil failure development below the base of the excavation can’t be accounted for by the procedure used by Terzaghi and Peck (1967) diagrams. The equation of Henkel (1971) was used for the calculation of the value of KA and the maximum pressure ordinate for the case of soft to medium clay.

The coefficient of total stress earth pressure has been evaluated by using Henkel’s equation

where

d = depth of the failure surface below the cut,

Su = undrained shear strength of the soil

Sub = strength of the soil providing bearing resistance

Henkel has provided the following solution for the case of unloading at the surfaces of the ground

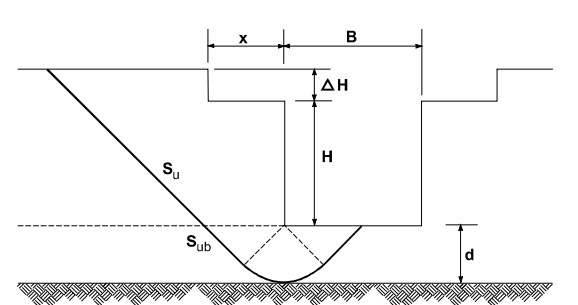
Figure 19: Henkel’s mechanism of base failure.

The values of KA have been calculated by using Henkel’s method at various ratios of d/H. figure 29 showed the results for Su = Sub.  It has been illustrated in figure that for 4<Ns<6, with the value of m=0.4 for the Terzaghi and Peck envelope, which is found to be more conservative concerning Henkel’s value. The validity of the Henkel equation is not applied for Ns<5.14 and the calculated earth pressure is found to be low unrealistically by using m=1.0.

The maximum pressure ordinate can be evaluated by using the KA= 0.22 for the range of 4<Ns<5.14. Particularly for the transition states of soft to medium clay and stiff to hard clay or for Ns=4. The total load is about 0.193γH² for the KA= 0.22 by using soft to medium clay. The stiff to hard fissured clay on the earth pressure diagram has a maximum pressure ordinate of about 0.26γH.

However, Henkel's method is found to be limited for the cases where the retained side clay soils can be characterized by using the undrained shear strength value constantly. The methods of limit equilibrium are preferred when profiles with more detailed shear strengths are required (Neelakantan and Richards, 1992).

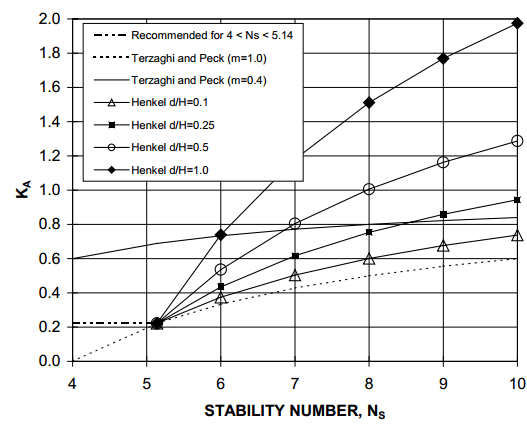
Figure 20: Value of KA based on Terzaghi and Peck envelope and Henkel’s method.

Design analysis

Homogenous profiles of soil are considered while describing the earth pressure diagrams in the above sections. Thus considering the stratified soil deposits, the methods are difficult to adopt. For stratified soil, a method of redistributing the earth pressures can be used and recommended. The soil profiles which are subjected to the surface failure are not suitable for such methods, particularly where the irregular surcharge loading is observed. The method has been described through the following points.

The pressure exerted over the height of excavation can be evaluated along with the evaluation of the load subjected to the soils by these active earth pressures. Other conventional methods of geotechnical engineering can be applied for the analysis of the total earth pressures by applying the assumption of the shear strength mobilization of the soil (Ostermayer, 1974; Prakash and Basavanna, 1969). Another method called trial wedge stability analysis can be applied in the case of irregular loading of surcharge, irregular surfaces and complicated stratification.

The total determined load is required to be increased by the factor of 1.3 for the sheet pile walls or the anchored beams. Where the control of deformations is required strictly a greater value is always recommended for the total load.

Trapezoidal distribution can be used for the even distribution of the factored force for the pressure diagrams.

In the presence of the irregular surcharge or deep seating of the potential failure surfaces, the limit equilibrium methods are recommended for the calculation of the earth pressure loadings (Reese, 1958).  

Sliding Wedge Analysis Method

The total required horizontal load can be calculated by applying the sliding wedge analysis which is an equilibrium method. For a wall of height H, a figure has been presented for a free body and force vector illustrations. The soil used has been characterized by the front and behind the wall with the effective stress angle of friction φ’. The anchor bond zone is assumed for the failure surfaces to be passed in front of them and full loads of anchors are contributing to the stability of the wall. The target factor of safety has been used to factor the shear strength i.e.

φ’mob=tan-1 (tanφ’/FS).

Over the embedment depth of the wall has been assumed for the passive resistance. The passive earth coefficient of pressure has been calculated by using the interface friction angle δ that is equal to the φ’mob.

Analysis

The external horizontal force has been represented by the PREQ in the figure and the stability has been provided in the vertical cut. The horizontal component of the anchor forces i.e. T cos I and the embedded wall portion lateral resistance SPH are used to represent this force. The horizontal assumption of the PREQ suggests that the soldier beam has provided the vertical resistance SPV which is found to be opposite in sign but equal in magnitude to loads of the ground anchors and their vertical components, T sin i. 

The resisting force for, PREQ, can be calculated as follows.

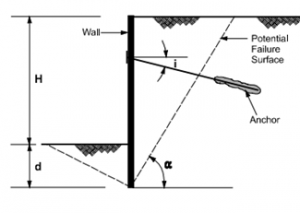
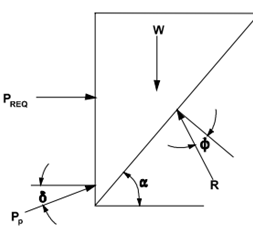
Figure 21: ground anchor wall system                                            Figure 22: free body diagram

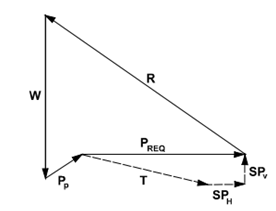
Figure 23: force vectors

Figures: Force equilibrium method for anchored walls (after FHWA-RD-98-065, 1998).

The iterative procedure has been adopted to find the solution and the angle of potential failure of the surface has been adjusted and the depth of the wall embedment has been found. In the apparent pressure envelop the load PREQ is then redistributed for the calculation of loads of the ground anchors and the moments of bending for the walls with its exposed portions.

Water Pressures

The large water loads are required to be resisted by designing the lagging walls and permanent anchor retaining walls. The retained soil at the surface of the drainage can be collected at the wall tops through ditches for systems of the walls. The prefabricated drainage elements have been used for the collection of the water from the subsurface. Such elements can be placed between the wall ending and top surfaces (Reese and Koop, 1974).

The associated water forces for the seepage residing beneath and behind the walls are important to be resisted particularly for the temporary systems. For the homogenous soil, a flower has been illustrated for typical retaining walls in the figure. The calculations of the pressure of pore-water are simplified by making important assumptions including the uniform dissipation of the head difference (H+i-j) through the flow path (2d+H-i-j) which is the shortest potential flow path.  

Such paths are found to be run down through the back and front of the wall. The calculated pressure of the pre-water has increased pressures more than the hydrostatic pressures of the front walls and is lesser than the hydrostatic pressures behind the wall as illustrated in the figure.

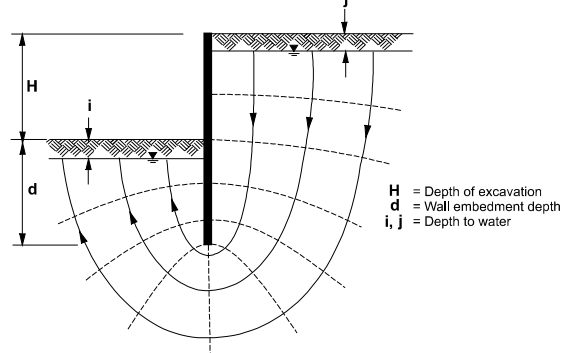
Figure 24: flow net for anchor retaining walls source (CIRIA 1984)

As shown in the figure the bottom pressure of the wall is equal to the pressure on either side of the wall. Where the Uf value is given by the following equation

The pressure acting on the wall has been shown in figure b. the largest water pressure is occurred at the water table level through the excavation and is given by:

The no seepage condition of net water pressure has also been illustrated in the figure for efficient comparison.

Where the net pressure has been calculated by the following equation

On pore water pressures the effects of the conditions of the special drainage have been assessed by using seepage flow nets. The pore-water pressures are found to be varied greatly with the variations in the distances behind the wall and when the wall acts as a pure drain.

However, the procedure shown in the figure is not sufficient for the accurate calculations of the pressures behind the wall. Thus for normal designing, the flowers which are simplified can be used and assessed (Richards and Elms, 1992).

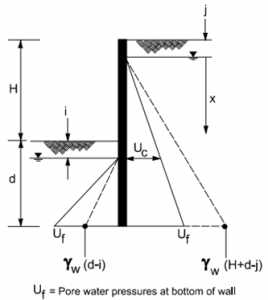
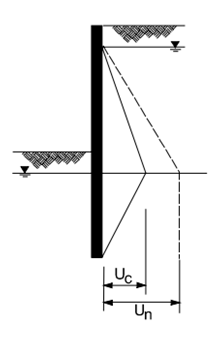
Figure 25: net water pressure                          Figure 26: gross water pressure

Source: (CIRIA 1984)      

Example

 Wall requirements

With the following characteristic parameters of the soil

A large lag of 1.5 m has been observed between the water table behind the wall and the water table in front. For the anchored wall, the force in each tie road is required to be measured by using traditional methods. The depth of embedment is also required to be measured by using the limit state method.

Where

Force

The pressure distribution has been shown in figure 27; the net water pressure is estimated at point C.

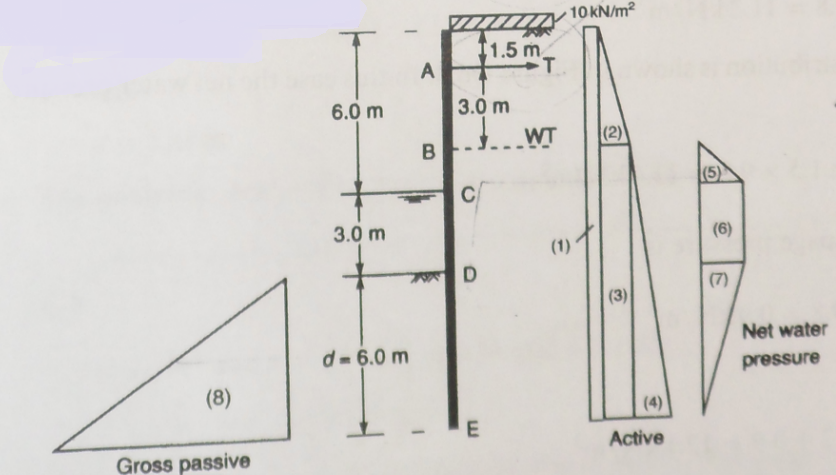
Figure 27: example wall

• Net water pressure:

• Average seepage pressure

Hence:

By considering the moments about the anchor point A in figure

Available passive resistance

Factor of safety

Force in each tie

Therefore

The surcharge is a variable action thus applies a partial factor of about 1.30 to the force (1)

In this calculation, depth d has been estimated

Minimum depth embedment

By trial,

The minimum depth of embedment required is 5.44m

Results

The loads applied at the ground surface vertically are called surcharge loads and have been assumed to increase the lateral stresses uniformly throughout the wall height. For uniform surcharge loading, the increase in lateral stress can be evaluated by using the following equation (Romanoff, 1957)

Where:

∆σh = increase in lateral earth pressure due to the vertical surcharge load,

qs = vertical surcharge stress applied at the ground surface,

 K =an appropriate earth pressure coefficient. 

Standard SI units are: 

∆σh (kPa), K (dimensionless), and qs (kPa)

 For the system of highway walls, the examples of the surcharge loads can be taken by including

• By considering the approach of the bridge weight and concrete pavements the resulting dead load surcharges can be evaluated
• Due to the traffic loadings, the load surcharges include live load surcharges
• During the construction of the system of the anchored walls, another surcharge was included due to the storage of material and equipment.

The anchor retaining wall has been expected to be designed for the pressure of the live load surcharge of the value of about 12 kPa when the traffic is assumed to be at the distance from the face of the wall that is equivalent to the ½ of the height of the given wall (AASHTO, 1996). 

As compared to the surcharge loads, the line loads, strip loads and point loads are considered to be the vertical loadings that are being applied to the limited areas. The wall system design uses the lateral earth pressure increase which is not found to be constant with varying depths even for the case of the uniform surcharge loadings. 

The equations of elasticity theory for the distribution of the lateral stresses have been considered for the calculation of these loadings (NAVFAC, 1982). The design earth pressure envelops are then added with the lateral pressures that have been resulted from the surcharges.

10‑2 Presumptive average ultimate bond stress for ground/grout interface along anchor bond zone (after PTI, 1996)

Discussions

Using the method of tributary area calculations the horizontal anchor loads can be calculated by employing the hinge method as shown in the figure for multilevel and one level anchor retaining walls. It has been assumed for both methods that the zero bending moment at the hinge is developed for the sub-grade of the excavation where the subgrade of excavation acts as a strut. The walls that penetrate the competent materials are found to be more supportive of the latter assumption. The design of the wall that can be controlled by the maximum bending moment is typically measured for the exposed portions of the wall for instance above the subgrade of excavation (Romanoff, 1972; Sharma, 1994).

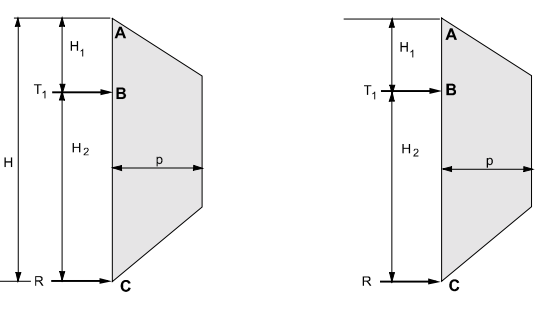
Figure 28: Tributary area method and hinge method

T₁ = load over length H1+H2/2                                             T1 calculated from

R = load over length H2/2                                                      R = total earth pressure - 1

For those walls which have been constructed into the competent materials, a factor called reaction factors has been introduced to support the passive resistance of the given soil below the subgrade of the excavation. To develop the passive resistance the wall is required to be embedded significantly.  The apparent pressure diagram area has been considered as a tributary area which is carried by the lowest anchors. Considering the apparent pressure diagram the reaction force is thus equivalent to the anchor load (Siller, 1992).

The data has been exhibited for the excavation base to the middle of the anchor or between the excavation base and the lowest end of the anchor. For the penetration of the weak materials, the walls are required to have sufficient passive capacity below the excavation base which is not readily available for resisting the immediate reaction forces which are independent of the depth of the wall embedment.

The lowest anchors have been designed for carrying the same loads as discussed above. The lowest anchor also has to respond to the load in response to the reaction force. The foundation of the beam on elastic or the interaction of the soil and structure can be analyzed for the continuous design of the beams which have small reaction toe (Siller and Frawley, 1992).

The values have been calculated by using the following figures. Where the anchor loads are taken as the horizontal component of the anchor/wall width T_hi. The total load for horizontal anchor T_h was then calculated as

The horizontal spacing between two anchors is denoted as s and T as an anchor load which has been used for designing the anchor bond zone.

The design load was then calculated as

Where  

θ = angle of inclination of the anchor below the horizontal.

The total anchor load has been calculated by using its total anchor load which is denoted as Tv.

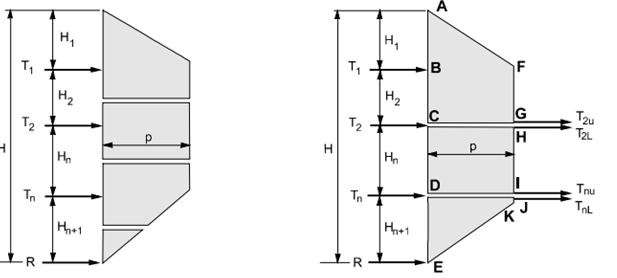
Figure 29: Tributary area method and hinge method

T₁ = load over length H1+H2/2                                    T1 calculated from

T₂ = load over length H2/2+Hn/2                                   T2u= total earth pressure (ABCGF)-T1

T_n = load over length Hn/2+Hn+1/2                              T2L = calculated from

R = load over length Hn+1/2                                          Tnu = total earth pressure (CDIH)-T2L

                                                                                        TnL = calculated from

                                                                                        R = total earth pressure – T1- T2- Tn

                                                                                        T2 = T2u+T2L

                                                                                         Tn = Tnu+TnL

For strand tendons, the minimum length unbounded for the soil and rock is found to be 4.5m however the value is 3m for bar tendons. A significant reduction in load can be prevented by such minimum values that have been resulted from the losses of seating during load transfer to the structure that has been followed by the testing of the anchor load. The longer lengths which are unbounded are usually required to

• Minimum distance for the critical potential failure for the location of the bond length
• Anchoring in the appropriate ground for the location of the anchor bond zone
• To ensure the stability of the system of the anchored system completely
• For the accommodation of the long term movements

In other words, behind the critical surface of the potential failure, the unbonded length can be extended to the minimum distance of about H/5 or 1.5 m. The extension has been made for the accommodation of the transfer of the minor loads to the grout column for the top bond zone of the anchored wall (Skempton, 1964).

The unbounded zone and the anchor bond zones have been grouted in one stage for maintaining the stability of the hole and for the creation of the grout cover which must be continuous against corrosion protection (Terzaghi, 1954). The large diameters of the anchors in which their unbounded length has been extended behind the critical surface of the potential failure offer significant strains at the top zones of the anchor bonds that have caused the transfer of the load throughout the grout column and above the bond zone of the anchor.

There are two stages in which anchors of larger diameters have been grouted. In the two-stage grouting system, the anchor will be tested and the bond length will be grouted under stage one. While in stage two the length portion of the drill hole which is unbounded was grouted and then the anchor was tested for its performance. Due to the chances of the local collapse the procedure of two-stage grouting has not been recommended which has to be accommodated by compromising the corrosion protection strategies of the grout.

Previous field experiences have been considered for the estimation of the capacity of the load transfer for the anchor bond lengths. By using the results of previous fields the capacities have been estimated and potential variations in the capacity have been accommodated.

The variations arise due to the differences in the grouting methods, installation procedures and corrosion protection techniques. in the soil deposits of given characteristics, the field capacity is found to be dependent greatly on the different drilling methods i.e. drill hole quality, cleaning procedures and the time for which the drill hole was kept open (Weatherby, 1998).

The pressures and the various methods used for the purpose of grouting are dependent upon the diameter of the drill hole and the length of the bond zone of the anchor retaining wall. These items should be left for the discretion of the speciality anchor contractor excluding the certain minimum values. The minimum anchor capacity is required to be designed as the main responsibility of the designer to achieve the given ground type.

The capacity of these tendons of anchored walls can be handled without the introduction of specialized or heavy equipment. One or two workers can be assigned to handle the stressing equipment without any aid of the lifting equipment mechanically (Whitman, 1990). The diameter of the drill is not more than 150mm except for the hollow stem anchors that have been approximated for 300 mm diameters approximately.

Few anchored walls are restricted to the length of 9 m to comply with the geometrical or geotechnical requirements. For bar tendons, the minimum length has been maintained up to 3 m and for the strand tendons, the length is about 4.5 m. the acceptable reduction of the load has been avoided by adopting these minimum unbounded lengths. These minimizations result from the losses due to the seating during load transformation and other pre stress losses because of the creeping phenomena in the prestressing soil or steel (Wright, 1995).

The load transferred from the bond length to the soil has been estimated for the smaller values of the diameters, lesser densities and straight shaft anchors which are gravity grouted particularly for the preliminary design parameters. In soil, the maximum allowable design load for anchor retaining walls are determined by multiplication of the ultimate transfer loads to the bond lengths and then dividing the product by a factor of safety 2.0

11‑3 Presumptive ultimate values of load transfer for preliminary design of small diameter straight shaft gravity-grouted ground anchors in soil.

Note: (1) SPT values are corrected for overburden pressure.

For post grouted soils, gravity grouted and pressure grouted soils the lengths of the anchor bonds are typically found to range from 4.5-12 m. A significant increase in the capacity has been observed for the lengths of the bonds which are about 12 m by deploying the specialized methods for transferring loads from the top of the anchored retaining walls towards the bottom end. The anchor bond zones are taken as the function of surface tension thus the initial increments of the load transferred to the anchored walls have to be resisted through the soil present at the top of the anchor bond zone due to the presence of the strains of the upper grout body as illustrated in figure

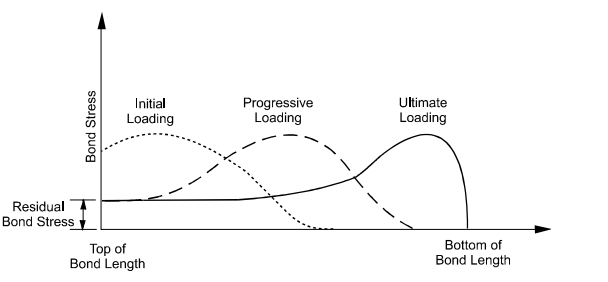
Figure 30: mobilization of the bond stress for anchors

The normal stresses applied onto the body of the grout have significantly increased the pressure groundings particularly in the cohesionless soils which increase the confinement. The effective diameter has also been observed significantly for the small increase in it and specifically for the anchor bond zone. However, the estimates of the capacity are based on the hole diameters as-drilled.

The gravity grouted bond stress values that have been estimated are illustrated in the table which shows data for the pressure grouted soil anchors as well. The variations in the ultimate values are thus quite obvious from these values. Reviewing the ultimate bond stress values, it is important to consider that the values are not necessarily required to be implied correspondingly for a larger capacity of anchors per unit length.

The hollow stem anchors for example can be considered for their more capacity per unit length than that of their smaller diameters. The bond stress values are not argued for the anchor diameter but the post grouted anchor. The capacity of the cohesive soils can be increased by increasing the pressure grouting.  On the other hand in cohesive soils, the capacity can be increased by deploying the post grouting phenomenon (Xanthakos, 1991).

The redial stresses act upon the body of the grout which can be increased by the post grouting and thus develop an irregular surface around the length of the bond that is able enough to lock the ground and the grout. In the post grouted anchors the load capacity is difficult to be predicted that resulting in the complexity of the procedures of the anchor grouting. However, the load capacity can be increased by post grouting the ground anchors. The load capacity can be increased up to 20-50 per cent per phase with the common limit of three phases for the post grouting.

A bond length of about 3-10m has been evaluated for the rock anchors while maintaining the minimum bond length of about 3m. The load transfer has been observed from the bond length to the sound rock competitively which can be estimated through the various types of rocks.

A geologist may input a lower value especially when the strength of the rock mass has to be controlled by the discontinuities in the structure. In competent-rock, the maximum design load of the anchor can be determined by multiplying the ultimate transfer loads to the bond lengths and then dividing the whole term by the safety factor of 3.0.  

When compared with soil the factor of safety have a higher value which is because of accounting for the uncertainties associated with the rock mass and its potential discontinuities including fractures, joints and clay-filled fissures. The clay shales which are an example of the weak rock the transfer of bond stress is found to be relatively uniform when compared with the value transferred in more competent rocks. Intermediate geometry is a common term used for these weak rocks which have unconfined compressive strength which varies from 0.5-5.0 MPa.  The anchor bond lengths of these materials can be evaluated by defining the design values and the safety factors of about 2.0 for the transfer values of ultimate loads.

11‑4 Presumptive ultimate values of load transfer for preliminary design of ground anchors in the rock

For the interface of rock and grout, the measured ultimate bond stress ranges are illustrated in table7. It has been suggested by PTI (1996) that the rock and grout interfaces can be approximated for their ultimate bond stresses up to 10% of the rock’s compressive strength which is unconfined and up to the maximum ultimate bond stress value which is 3.1 MPa.

An implicit assumption has been made for the calculation of the bond length which states the uniform mobilization of the bond at the interface of the rock and grout. The case is however unlikely to occur unless the bond zone has been expected to be formed in the weak or soft rock.

In the case of the competent rock where the ratio of the elastic modulus of the grout and the rock is lesser than 1, the load is found to be transferred in the upper 1.5-3m of the bond zone of the anchor from tendon to the rock. An additional margin of safety can also be provided by considering the additional bond length of the anchor zone. Thus the values which are required for resisting the design loads are always greater than the calculated lengths.

13.     Conclusion

In anchored systems, the ground anchors are always designed by making assumptions of carrying a tributary load area by the anchors that are based on the vertical and horizontal spacing between two adjacent anchor retaining walls. It is important to ensure that the designed ground anchors are capable enough to carry the loads throughout their life spans.

The strength can be evaluated by the strength of the anchor tendon, length and diameter of the anchor, procedures of grouting and drilling and many more. Depending upon the specific requirements of the projects the vertical and horizontal spacing will be varied according to the project constraints. Such requirements and constraints of the project may include

• Requirement of designing a highly stiff system for example the spacing between the anchors is very low so that the lateral wall movement can be controlled.
• The structure which already exists and may affect the inclination and positioning of the newly developed anchors
• Categories of the wall elements which have been selected for the given design

The uppermost ground anchor can be evaluated for its vertical positioning by considering the cantilever deformation of the anchored wall which must be allowable. The potential for exceeding the passive capacity can be minimized by selecting the vertical position of the uppermost anchor. The movement of the wall results in the retained grounds when the anchors are loaded 133% of the loading design during load testing.

When the uppermost ground anchor is designed relatively larger for the design load then the load must be resisted for landslides and large surcharges. The passive capacity is also found to be exceeded when the soils are relatively weak or disturbed. After the exceeding passive capacity, the sheet pile or soldier beams are found to be moved in the retained ground excessively.

Over the centre of the bond zone of anchor, a minimum overburden of about 4.5m is allowed as shown in the figure for the anchors retained in the soil. The method is found to be useful in the prevention of grout leakage while installing pressure grouted anchors. The system will also be helpful to prevent the heave that is resulted from the large pressures of grouting at the ground surfaces.

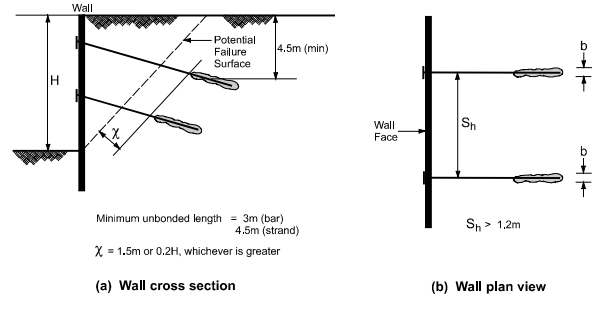
Figure 31: Vertical and horizontal anchor retaining walls

The individual loads of the ground anchors and flexural capacity of individual sheet piles or soldier beams are responsible for defining the horizontal spacing between two anchors.  For driven soldier beams typical horizontal spacing is found to be 1.5-3m and for drilled in soldier beam is 3m.

The figure shows a minimum horizontal spacing between the adjacent anchors that indicated that a group effect can be minimized at the anchor intersection and between the adjacent ground anchors by avoiding the deviations of drilling. The load-carrying capacity can be reduced by deploying the group effects of the individual ground anchors.

References

1. Abramson, L. W., Boyce, G. M., Lee, T. S., Sharma, S. (1993). "Advanced Course on Soil Slope Stability: Volume I, Slope Stability Manual.” Report FHWA-SA-94-005, Federal Highway Administration, Washington, D.C.
2. American Society of Civil Engineers (1994) "Guidelines of Practice for Braced and Tied-back Excavations” Geotechnical Special Publication No. 74
3. Andersen, T.C. (1984). "Earth Retention Systems, Temporary and Permanent, Meeting Preprint.”Proceedings of the 32nd Annual Soil Mechanics and Foundation Engineering Conference, Minneapolis, Minn
4. Barley, A.D. (1997) “Discussion Session 3” Proceedings of the International Conference on Ground Anchorages and Anchored Structures, Thomas Telford Publishing, London, U.K., pp. 572
5. Bruce, D.A. (1997). "The Stabilization of Concrete Dams by Post-Tensioned Rock Anchors: The State of American Practice.” Proceedings of the International Conference on Ground Anchorages and Anchored Structures” Thomas Telford Publishing, London, U.K., pp  508-521
6. Bruen, M.P., Pansic, N., Schwartz, M.I. (1996). "Creeping Suspicion” Civil Engineering, ASCE, May, pp. 60-63.
7. Christian, J.T. (1989). “Design of Lateral Support Systems” Proceedings, Seminar on Design, Construction, and Performance of Deep Excavations in Urban Area, Boston Society of Civil Engineers Section, ASCE
8. CIRIA (1980). Design and Construction of Ground Anchors, 2nd ed, Construction Industry Research and Information Association, Report 65, London, U.K
9. FHWA (1986). "Recommendations for Monitoring Applied Load During Permanent Anchor Testing.” Geotechnical Engineering Notebook, Geotechnical Guideline No. 12, Federal Highway Administration, Washington, D.C.
10. Golder, H.Q., Gould, J.P., Lambe, T.W., Tschebotarioff, G.P., Wilson, S.D. (1970), “Predicted Performance of Braced Excavations,” Journal of the Soil Mechanics and Foundations Division, ASCE, Vol, 96, No, SM3, pp. 801-836.
11. Hanna, T.H. (1982). Foundations in Tension, Ground Anchors, McGraw-Hill Book Company, Inc., New York, N.Y
12. Institution of Civil Engineers (1997), Proceedings of the International Conference on Ground Anchorages and Anchored Structures, G.S. Littlejohn, Ed., Thomas Telford Publishing, London, U.K. 644 p
13. Littlejohn, S (1992) “Ground Anchorage Technology - A Forward Look." Proceedings of the Conference on Grouting, Soil Improvement and GeoSynthetics, Vol. 1, Geotechnical Special Publication No. 30, ASCE, New Orleans, Louisiana, pp. 39-62
14. Ludwig, H.P. and Weatherby, D.E. (1989), "Behavior of a Tieback in Cohesive Soil” Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, A.A. Balkema, Brookfield, VT, pp. 1023-1026.
15. Neelakantan, G., and Richards, R., Jr. (1992). "Balanced Seismic Design of Anchored Retaining Walls," Journal of Geotechnical Engineering, ASCE, Vol. 118, No. 6, pp. 873-888.
16. Ostermayer, H. (1974). "Construction, Carrying Behavior and Creep Characteristics of Ground Anchors” Proceedings of the Conference on Diaphragm Walls and Anchorages, Institution of Civil Engineers, London, England, pp. 141-151.
17. Prakash, S. and Basavanna, B.M. (1969), "Earth Pressure Distribution Behind Retaining Walls During Earthquakes.” Proceedings of the 4th World Conference on Earthquake Engineering, Santiago, Chile
18. Reese, L.C. (1958). Discussion of "Soil Modulus for Laterally Loaded Piles.” by McClelland and Focht, Transactions, ASCE, Vol. 123, pp. 1071-1074.
19. Reese, L.C., Cox, W.R. and Koop, F.D. (1974), "Field Testing and Analysis of Laterally Loaded Piles in Sand.” Paper No. OTC 2080, Proceedings of the 5th Offshore Technology Conference, Vol. II, Houston, Texas.
20. Richards, R. Jr., and Elms, D.G. (1992), "Seismic Passive Resistance of Tied-Back Walls," Journal of Geotechnical Engineering, ASCE, Vol. 118, No. 7., pp. 996-1011.
21. Romanoff, M. (1957), Underground Corrosion, Circular 579, National Bureau of Standards
22. Romanoff, M. (1972), “Corrosion of Steel Pilings in Soils” Contained in National Bureau of Standards Monogram 127, NBS Papers on Underground Corrosion of Steel Pilings (1962-1972).
23. Sharma, S. (1994) "XSTABL, An Integrated Slope Stability Analysis Program for Personal Computers.” Interactive Software Designs, Inc., Moscow, Idaho
24. Siller, T.J. (1992) "Design of Tied-Back Walls for Seismic Loading" Journal of Geotechnical Engineering, ASCE, Vol. 118, No. 11, pp. 1804-1821.
25. Siller, T.J., and Frawley, D.D. (1992) "Seismic Response of Multianchored Retaining Walls" Journal of Geotechnical Engineering, ASCE, Vol. 118, No. 11, pp. 1787-1803
26. Skempton, A.W. (1964). "Long-Term Stability of Clay Slopes” Geotechnique, Vol. 14, No. 2, pp. 75-101
27. Terzaghi, K. (1954). "Anchored Bulkheads” Transactions, ASCE, Vol. 119
28. Weatherby, D.E. (1998). “Summary Report of Research on Permanent Ground Anchor Walls, Vol. 4, Conclusions and Recommendations” Report FHWA-RD-98-068, Federal Highway Administration, McLean, VA.
29. Whitman, R.V. (1990). "Seismic Design of Gravity Retaining Walls” Proceedings of the Conference on the Design and Performance of Earth Retaining Structures, Geotechnical Special Publication No. 25, ASCE, pp. 817-842.
30. Wright, S. (1995). "UTEXAS3, A Computer Program for Slope Stability Calculation - User's Manual." Shinoak Software, Austin, Texas
31. Xanthakos, P.P. (1991). Ground Anchors and Anchored Structures. John Wiley & Sons, Inc., New York, NY.