Applied Corporate Strategy
July 9, 2022
Case of Tesla Merger with Solar City
July 9, 2022
Background/ Introduction
Primarily, this study will analyze a summary of the Investment Policy Statement of Miss I. Ohri, stating the objectives of her investment strategy and her future investment plans as well. Secondly, this study will put the shade on constructing a Portfolio using UK FTSE 100 stocks and UK Government Bonds. Therefore, it will be critically analyzed the investment benefits in FTSE 30 stocks using the correlation analysis (Barberis, Mukherjee, & Wang, 2016). This will be done by looking at all the necessary information gathered (downloading share prices of UK FTSE 100 stocks data for the last 11 years). Furthermore, it will be analyzed the Covariance, Correlation, Regression, and Descriptive Statistics of the constructed portfolio of 100 stocks, using data–Data Analysis, and also will be analyzed for the 100 stocks' Returns and Excess Returns. These calculations, especially the correlation analysis will allow us to select the best 30 stocks from UK FTSE 100 stocks. Thirdly, it will be demonstrated how to calculate the Optimum Risky assets using the Markowitz Portfolio Optimization Model and the Traynor-Black Model, and then will be assessed the portfolios’ returns, based on 10-year performance and in the end, will be analyzed the concrete performance for the last year( Lasher,2013).
Investment Policy Statement
What is an “Investment Policy Statement” – IPS?
An Investment Policy Statement (IPS) is a manuscript enlisted amongst a portfolio manager and a client that summarizes broad-spectrum strategies for the manager. This declaration specifies the overall investment goalmouths and purposes of a client and defines the tactics that the manager would involve to meet these objectives. There is exclusive information on stuff such as asset allocation, risk tolerance, and liquidity necessities that are included in an IPS. (Investopedia, 2017). An example of an Investment Policy Statement will be described as follows:
Investment Policy Statement (IPS)
Client name: Iva Ohri
Status: (Single)
Age: 35
Retirement age: 65 years old
Address: 9 Stevenage Road, East Ham, London
Postal Code: E62AU
e-mail: i
………………………………………………………………………………………………………………………………………
Investor Conditions
Due to the investors’ actual studies in MSc in Global Investments and Finance in London, actually, she isn’t interested in buying a new house, but she is interested in investing in other stocks and the money saved should be managed consequently for 5 entire years (Andersen, & Glenn,2014).
The Investor defines their understanding of investments as limited.
The predictable position for the Investors’ economic condition:
Modesty adverse over the next year (because of her studies);
Modesty optimistic over the next five years;
Very positive over the next ten years.
Iva Ohri currently is living in London, following her studies. She is paying a monthly rent of £500. Her monthly expenses are approximately £850. In addition to the money saved by her (approximately £7000), she owns another savings account in Albania.
…………………………………………………………………………………………………………………………………………
Overview
The following facts are a summary of the Investor outline, created based on the evidence that she provided:
Twelve-monthly family income (before tax) is £10,000 to £15,000;
Possibly will tolerate a provisional decline in her portfolio over one year of -4%;
She has some investment knowledge;
Her existing investment portfolio is embraced equal amounts of fixed profits and securities.
Investment Aims/Objectives
The Investor’s principal objective for the investment portfolio is to produce profits investing in properties in London and to achieve growth.
Investor’s Risk Tolerance: Traditional
Investment Time Horizon
She has acknowledged her portfolio’s investment time horizon to be 10 – 20 years.
Chapter 2: Methodology
The Methodology that will be used in this research will be a descriptive statistic and critical thinking of the calculations made with an Excel Sheet for calculating the Optimum Portfolio risky assets for UK FTSE 100 stocks. Also, it will be calculated the proportion of an Individual Investor portfolio that should be invested in the risk-free asset portfolio and the risk-free asset (Bodie, et. al, 2014).
How do we evaluate the Portfolio Performance of FTSE 100 stocks?
Firstly, we will download all the data of UK FTSE 100 stocks for the last 11 years and we will “copy” and “paste in the Excel Sheet all the FTSE 100 closing dates. Then, it will be calculated the returns of the portfolio for 11 years period, it will be calculated the standard deviation of the portfolio, the portfolio returns, the expected returns of the portfolio, the annual rate of each stock in the portfolio, the variance/ covariance matrix, annual variance, the annual standard deviation, the weighted portfolio, and the optimal risky portfolio. Below, will be shown step-by-step calculations that have been used in Excel Sheet, so you can have a better picture of the Optimum Portfolio.
Step 1:
Our Benchmark will be to divide the last year's performance (2016) and then the ten-year performance it will be shown together in the table. It will be calculated the holding period returns of 100 stocks, using the formula in Excel: So, we will convert the prices into returns using the formula:
Rt = LN (Pt/Pt-1);
In Excel Sheet, the formula must be: =LN(price today/price yesterday) and then auto-fill the column. For UK Gilt, for example, the formula that will be used is =((1+(Data!B3/100))^(1/12))-1 because we want to exclude UK Gilt when constructing our portfolio. For FTSE 100, the formula for calculating the returns over the 10 years is: =LN(Data!C3/Data!C4)
Step 2:
How to find the covariance and variance for 100 stocks?
It will be found it running Data – Data Analysis – Selecting Covariance and then selecting all the data with the returns for 100 stocks and then run ok. The same thing we will do also for finding the Variance of 100 stocks ‘returns Portfolio, running Data – Data Analysis -Selecting Variance, and then selecting all the Returns data of 100 stocks and then pressing ok. Correlation means how all the 100 stocks’ returns occur simultaneously. We also need to find the regression of our portfolio running Data – Data Analysis – Regression – select all the Returns data of 100 stocks and then press ok.
Step 3:
We have to choose 30 stocks, based on the correlation and alpha. To create an Active Portfolio, the correlation has to be lower enough. Below will be shown the 30 stocks based on the lowest correlations:
(30 Stocks Portfolio)
Ashtead Group |
RBS |
Aviva |
Barrat Developments |
GSK |
British American Tabacco |
LAMB |
ITV |
Persimmon |
Taylor Wimpey |
Wolesley |
Randgold |
HMSO |
TAG |
British Land |
Carnival Corporation & plc |
Easyjet |
BT Group |
Informa |
3i |
London Stock Exchange Group PLC |
Marks & Spenser Group PLC |
Sage Group |
Travis Perkins |
RELAX |
Old Mutual |
KGF |
DCC |
Intu |
Legal & General Group PLC |
Constructing Portfolio using Markowitz Optimization Model
Step 4:
After choosing the 30 Stocks Portfolio, it will be demonstrated how to calculate the Optimum Portfolio risky assets, using Excel. It will be shown the Portfolio Optimization of 30 Stocks portfolio using the Markowitz Portfolio Optimization Model. This Portfolio theory explains how each of the 30 stocks in a portfolio relates respectively with each other and it tries to find to reduce the risk while optimizing returns. What is important to consider in this Model is that we are going to look for the Optimal Portfolio, which will give us the best risk-return trade-off and that will lie along this minimum variance frontier within a given of risky assets.
In the Excel Sheet, It will be looked at 30 different stocks that we have already chosen, and we are going to combine those in the best weights, to give us that risk-return trade-off that produces the optimal outcome. So, the Expected Return for a portfolio is calculated as the weights of the assets within the portfolio multiplied by their Expected Return (Portfolio Optimization Youtube, 2017):
E(rp) = ∑ W1 E (ri)
The variance of two assets (X and Y) portfolio is calculated as: (the weight of “X” squared, multiplied by the variance of X squared, plus the weight of “Y” squared multiplied by the variance of Y, plus two times the weight of “X” multiplied by the weight of “Y”, multiplied by the covariance of X and Y or how they move together. So, if we will generalize this formula to more than 2 assets, we can use the following equation that is: the sum of the weights multiplied together for each asset “I” and “j” multiplied by the covariance. The Expected Return for the Portfolio is calculated using matrix notation, where we have the weights of the assets of
our Portfolio transposed multiplied by their expected return, where: W – is the vector of weights of the individual assets (i through j) in the Portfolio and R – is the vector of expected returns on the individual assets (i though j) in the portfolio. The Formula in Excel that will be used is:
{=mmult(transpose(W),R)}
Where W – is the Column of Weights and R- is the Column of Expected Returns. When we are making calculations with arrays in Excel, type in the formula, but don’t press Enter. Instead, we have to hold down [Ctrl] [Shift] and then press [Enter]. This will tell Excel that we are making calculations with an array and put the curly parentheses around the formula.
The Variance of the Portfolio is calculated as the weights of each asset in the Portfolio transposed multiplied by S, where “S” is the variance/covariance matrix and then multiplied again by the weights of the assets in the Portfolio.
The Standard Deviation of the Portfolio will be calculated as the square root of the variance of the Portfolio. The Standard Deviation of the returns of the Portfolio is calculated in Excel as:
{=sqrt(multi(multi(transpose(W),S),W))) and then Press [CTRL, SHIFT together and then press [Enter]]
The Optimal weights of the 30 Stocks in our Portfolio are the ones that maximize the value of the sharp ratio for the Portfolio, and it will be shown using “Solver” in Excel to do this.
The optimal mix of weights for the assets in our risky portfolio is the mix that creates a portfolio along the efficient frontier that is tangent with the capital allocation. This results in the capital allocation with the largest slope (sharp ratio) and is, therefore, the optimal risky portfolio.
We are going to choose the stocks that have the higher Sharp ratio, and the Risk-free rate we will assume will be 1,07.
The Complete Portfolio | |||
Risky portfolio | Gilt | Complete Portfolio | |
Expected return | 12.00% | 1.07% | 16.62% |
St.Dev | 14.52% | 0 | 20.66% |
A | 4 | Sharpe | |
Optimal weight: | 142.27% | -42.27% | 0.7527 |
Our Sharp ratio will be calculated in Excel as =(Expected Return – Risk-free rate)/Standard Deviation of the Portfolio.
So, the highest Sharp ratio in our 30 Stocks Portfolio is 0,752. And our Expected Return Portfolio is 12% with a Standard Deviation of 14, 52%.
Our Optimal Weight in our Risky Portfolio is 142.27% with a risk aversion of 4.
Also, if we look at our Complete Portfolio, our Expected Return is 16.62% with a Standard Deviation of 20, 66% (that is the measure of risk in our Portfolio), and an Optimal weight of 0.7527.
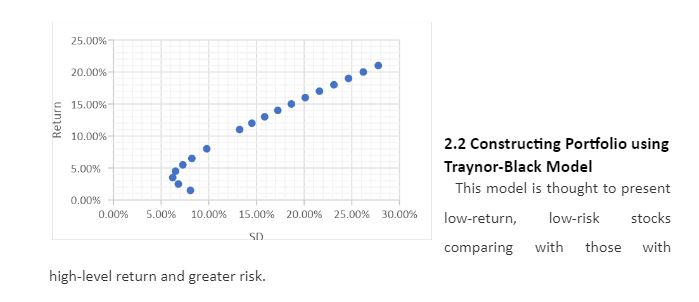
The portfolio we can find in the Graph below. The golden rule of an investor is that an Investor can take more risk investing in these 30 stocks, only if they can that higher level of return. And similarly, Investors can get a higher level of return if they are willing to take that extra risk (Mangram, 2013). No one the Investors should invest below of the 5% expected return because it will increase the returns while decreasing risk (Markowitz, 2014). So, the Graph shows that the lower the risk in a portfolio, the higher return. Investors should be interested in an efficient portfolio, which means a portfolio where the relationship between risk and return is such that we can get a higher return only by taking a little extra risk. And the Investor should be interested to take all this little extra risk because should bring a higher return (Markowitz, 2014). One thing that we want to know is, where the inefficient frontier end and the efficient portfolio start to do. Well, it is going to be the point on the graph below, where the Standard Deviation is the lowest (it is going to be the lowest risky portfolio) and we call this the Minimum Variance Portfolio (Mangram, 2013)
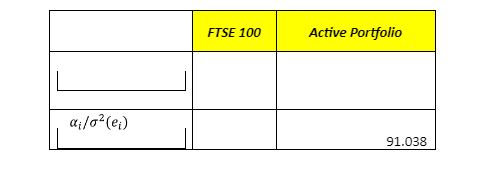
Constructing Portfolio using Traynor-Black Model
Advantages and disadvantages of using the Markowitz Optimization Model & Traynor-Black Model
The benefits of portfolio planning with the efficient frontier or the advantages of using the “Markowitz Optimization Model”, are wherever a portfolio’s risk and return and converted by the efficient frontier. The efficient frontier is an arched line that lies down in a graph with expected portfolio return on the “y” axis and the portfolio’s standard deviation (or risk) on the “x” axis. The Markowitz Optimization Model which is called the Modern Portfolio Theory is a methodology for portfolio investing, where the complete market and economy are investigated or analyzed. This theory is developed by Harry Markowitz (that is called the “father of portfolio management” (Wallengren, & Sigurdson, 2017)
This Portfolio Theory explains how each stock in a portfolio relates respectively with each other and it tries to find to diminish risk while optimizing returns. Model Portfolio Theory takes into account the revenues of collateral, as well as its systematic and unsystematic risk Mangram, 2013). So, it takes into consideration the whole return and risk of a portfolio consisting of specific collaterals, and it designs a line with completely the presented portfolio opportunities (Dhrymes, 2017). This line is recognized as the efficient frontier. The portfolio can accomplish better with a minimum quantity of risk, if based on risk and return a portfolio can move toward closer to the efficient frontier. To boost or optimize the risk and return, it is significant to invest in a portfolio that is on or lies down nearby to the efficient frontier. Everything that is underneath the efficient frontier yields requires too much risk for the expected return (Investopedia, 2017).
The “Treynor-Black Model” is a sort of asset allocation model that was established by Jack Treynor and Fischer Black. The model makes an effort to find out the optimal mixture of inactively and dynamically accomplished stocks in an investment portfolio. As soon as shaping the optimal allocation of stocks, the model concentrates mainly on stocks’ systematic and unsystematic risk (Gerber, Markowitz, & Pujara, 2015).
The disadvantage of using the Treynor-Black Model is that a specific individual can realize that the model concentrates less on the “Beta” of stock and its unsystematic risk. If a stock has more unsystematic risk, at that point it is not given not as much weight in the Treynor-Black Model (Gerber, Markowitz,& Pujara, 2015). As a consequence of this trend, this model is thought to present low-return, low-risk stocks compared with those with high-level returns and greater risk (Investopedia, 2017).
Chapter 3: Critically Analyse portfolios’ risk-return profiles
The analysis of portfolio risk-return profile is evaluated using the applicable model based on the 10-year performances and the abnormal returns for the previous year. Treynor-Black Model analyses the dimensional active investment as well as the asset allocation and market portfolio. The model is based on the fundamental assumptions that make the data apply otherwise it would be invalid. For instance, security analysts are involved in the active management of the organization and analyze the depth of the small number of stocks for the entire universe of securities (Brown, 2015).
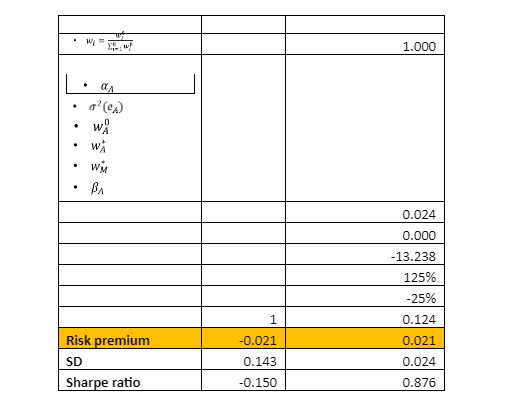
Treynor’s measure compares portfolios based on the alpha-to-beta ratio. The alpha of the FTSE security portfolio forecasted is 0 whereas the risk premium was -0.214 and the standard deviation of the portfolio stock is 0.1425. On the other hand, for the optimal risky portfolios, the values of the premium, standard deviation changes, and values of the Sharpe’s ratio. The values for the changes in the stock parameters with a beta of 1, risk premium of -0.021 standard deviation of 0.143, and -0.150.
Sharpe’s philosophy involves the regression of the portfolio returns on indices that represent a broad range of the assets clauses. Therefore, the regression coefficient of each index will assess the fund’s implicit allocation since the funds are restricted; the regression coefficients will be constrained to zero or positive and to an equivalent of 100 to have a complete asset allocation (Imai, Van Deventer, & Mesler, 2013). Since alpha is zero, it means that it is worthless to move away from the passive strategy and the index portfolio would solely depend on the managers’ choice of action but this is a far-fetched possibility. Therefore, determining the effect of the security purchase over the other involves the assessment of the Markowitz models that evaluate the risk, and returns and diversify the portfolio combination to neutralize the effect of the risk through diversification (Yang, & Yeh, 2015)
Chapter 4: Review Portfolio Performances
The assessment of the portfolio performance and effective rebalancing based on the remedial action involves the practical application of the Markowitz model whereby the investor can determine the trade-off between risks and returns ranging from zero to infinity. In this case, it is evident from the 100FTSE stock portfolio (Guerard, 2016). The mean return for the portfolio stock needs to be computed to determine using the weights of the respective portfolio (See FTSE 100 calculation)
Based on the attached values the expected portfolio returns is computed by wa*Ba+WbBb+…n =125%*0.124 +-25%*0.024 =0.155-0.006 =0.149.The evaluation of the risky nature of the portfolio involves assessing the beta stock of the portfolio and its implication to the investor. The optimal combination of the active portfolio with the passive portfolio takes off from the construction of an optimal risky portfolio from two risky assets that were evaluated through the application of Sharpe’s ratio (Brigham, & Ehrhardt, 2013).
The active portfolio is perfectly correlated with the index and requires diversification that involves mixing it with the index which is likely to yield higher returns. The success of the active management and the contribution of the active portfolio by the Sharpe ratio and the risky portfolio when compared to the index portfolio (Brown, 2015). Thus, in the assessment of the FTSE 100 portfolio stock indicates that diversification is the only available option to reduce the impact of the risk in the market scenario.
Analysis of the 30 Stocks Portfolio (2016)
The performance of the stock portfolio based on the FTSE market index indicates that nearly the beta of the portfolio ranges from 0.1-0.8 this indicates the risk aspect of the individual portfolio but the values reduces when diversified as evident in the combinations of their portfolio standard deviation. The implication of the portfolios st respective when each stock is analyzed by the corresponding alpha, beta, risk premium, and standard deviation parameters show that approximately 10 percent of the stock are less risky and approximately 40% are average whereas 50 percent of the stocks are highly risky which means that diversification method will be critical in reducing the impact of the risks.
References/Appendices
Andersen, K., & Glenn, P. (2014). Portfolio Preservation During Severe Market Corrections: A Market Timing Enhancement to Modern Portfolio Theory.
Barberis, N., Mukherjee, A., & Wang, B. (2016). Prospect theory and stock returns: an empirical test. The Review of Financial Studies, 29(11), 3068-3107.
Bodie, Z., Kane, A., & Marcus, A. J. (2014). Investments, 10e. McGraw-Hill Education.
Brigham, E. F., & Ehrhardt, M. C. (2013). Financial management: Theory & practice. Cengage Learning.
Brown, A. D. (2015). The Power of an Actively Managed Portfolio: an Empirical Example Using the Treynor-Black Model (Doctoral dissertation, The University of Mississippi).
Dhrymes, P. J. (2017). Portfolio Theory: Origins, Markowitz and CAPM Based Selection. In Portfolio Construction, Measurement, and Efficiency (pp. 39-48). Springer International Publishing
FTSE 100 Index, 2017. The online UK Stock Exchange Review. Available online at: www.ftse100.co.uk [Retrieved 12 August, 2017]
Gerber, S., Markowitz, H., & Pujara, P. (2015). Enhancing Multi-Asset Portfolio Construction Under Modern Portfolio Theory with a Robust Co-Movement Measure.
Google images, 2017. Image extracted from: Google/ipwatchdog.com [Retrieved 12 August, 2017]
Guerard Jr, J. B. (Ed.). (2016). Portfolio Construction, Measurement, and Efficiency: Essays in Honor of Jack Treynor. Springer.
Imai, K., Van Deventer, D. R., & Mesler, M. (2013). Advanced financial risk management: tools and techniques for integrated credit risk and Interest rate risk management.
Investment Policy Statement, 2017. Available online at: www.investopedia.com/terms/i/ips.asp [Retrieved 15 August, 2017]
Lasher, W. R. (2013). Practical financial management. Nelson Education.
Mangram, M. E. (2013). A simplified perspective of the Markowitz portfolio theory.
Markowitz, H. (2014). Mean–variance approximations to expected utility. European Journal of Operational Research, 234(2), 346-355.
Yang, S. S., & Yeh, Y. Y. (2015). Analysis of the Efficient Frontier for Life Settlements in the Presence of Longevity Risk. 財務金融學刊, 23(1), 1-29.
Wallengren, E., & Sigurdson, R. S. (2017). Markowitz portfolio theory.
Get 3+ Free Dissertation Topics within 24 hours?
