
Leadership Styles Practiced by Manager in LCCA
June 2, 2022
Key Innovation Management Models
June 2, 2022SPSS, or the Statistical Package for the Social Sciences, is a cornerstone tool in data analysis, renowned for its user-friendly interface and comprehensive statistical functions. Its intuitive graphical interface enables users to navigate through various statistical tests, data visualization techniques, and predictive modelling tools with ease. From basic descriptive statistics to advanced multivariate analyses, SPSS caters to a broad spectrum of analytical needs, making it an essential asset for researchers, analysts, and data scientists.
At its core, SPSS empowers users to uncover patterns, trends, and relationships hidden within complex datasets, facilitating evidence-based decision-making across diverse domains. Through features like regression analysis, factor analysis, and cluster analysis, SPSS enables analysts to identify dependencies and derive meaningful conclusions. Its ability to foster reproducibility and transparency in data analysis workflows further solidifies its position as a trusted tool for unlocking the potential of data and driving innovation in organizations worldwide.
Acknowledging the pivotal role that robust statistical tools play in extracting insights from complex datasets, let's delve into the exploration of data analysis using SPSS.
Introduction
This report presents a thorough data analysis conducted using SPSS software, focusing on assessing the impact of training on the accuracy of malaria detection through virtual microscopy. The dataset consists of 10 participants evenly distributed between a control group and a trained group. Initial and final scores from both groups were evaluated to ascertain the statistical significance of the training intervention. To examine the hypothesis of the model, an independent sample T-test was employed. Additionally, supplementary tests including normality tests, descriptive statistics, and box plots were utilized to enhance the comprehensive understanding of the data.
Understanding the context and significance of SPSS as a powerful statistical tool is essential before delving into data analysis.
Data Analysis
In this research, the data was obtained from 10 participants bifurcated into two groups: the control group and the trained group. The Control group included the individuals who were not provided training regarding virtual microscopy, and the trained group included participants who were given proper training after their initial score. The following table shows a summarized view of
the above table and states the value of the mean and standard deviation for the initial score and final score for the participants of the study. The mean value in the initial score is recorded to be 13.51, which is deviated by 1.64 units. On the other hand, in the case of the final score, the mean score was 56.5, which is higher than the former. It can be stated that overall, for both groups, the final results were significantly better than the initial score. The average final score deviated by 4.26 points.
Hypothesis
Following is the hypothesis that is being tested by this report:
- H0 = The mean values of the experimental group and control group after undergoing training regarding virtual microscopy will be equal
- H1 = The mean values of the experimental group and control group after undergoing training regarding virtual microscopy are not equal.
Normality Test
In the process of data analysis using SPSS, the normality tests hold strong significance. Normality tests were conducted on the data to assess whether or not the data was normally distributed (Park, 2015). Moreover, the normality was to be determined to evaluate which type of test was to be conducted. The following table shows the results of the normality test:

The null hypothesis for this test is that the data is normally distributed (Norusis, 2011). The null hypothesis has not been rejected for both the Kolmogorov-Smirnova or Shapiro-Wilk tests. This indicates that the information is normally distributed. Following is the Q-Q plot for the initial score:
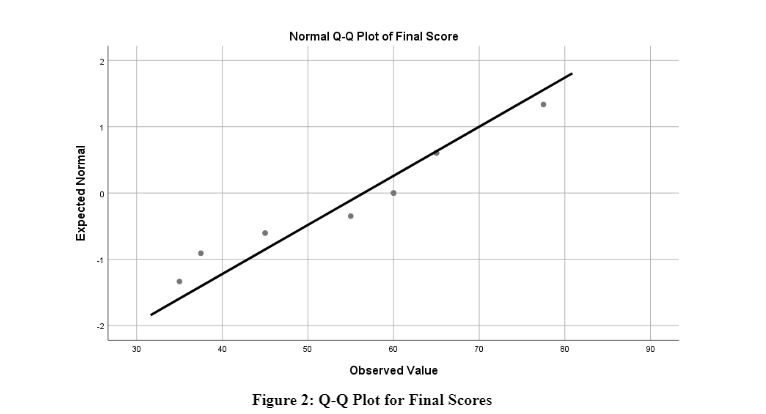
The above graph shows the observed values for the initial score plotted against the expected values. The graph shows an upward trend where most of the values are plotted within the line except for an outlier value. This further validates that the data for initial scores are normally distributed. The following graph shows the Q-Q plot for final scores:
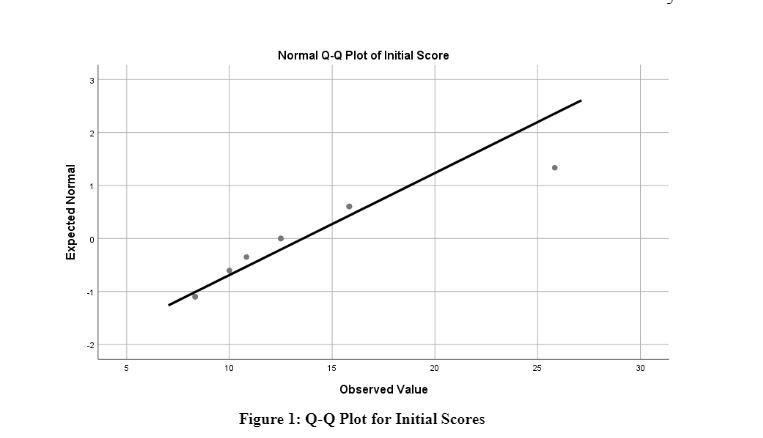
Figure 2: Q-Q Plot for Final Scores
The above graph shows the observed values for the final score plotted against the expected values. The graph shows an upward trend where most values are plotted within the line with no outliers. This further corroborates that the data for final scores are normally distributed. Moreover, from the normality test results, it can also be said that a parametric test can be applied to the model. Hence, an independent sample T-test will be used to test the main hypothesis of this research.
Box Plots
Box plots are employed to visualize numerical data groups based on quartiles in the dataset under consideration. They showcase five statistical values: maximum, minimum, first quartile, median, and third quartile, essential for data analysis using SPSS. Box plots are instrumental in determining data variability and identifying outliers (Kerr, Hall, and Kozub, 2002). The accompanying image illustrates the box plot representing the initial scores of the participants:
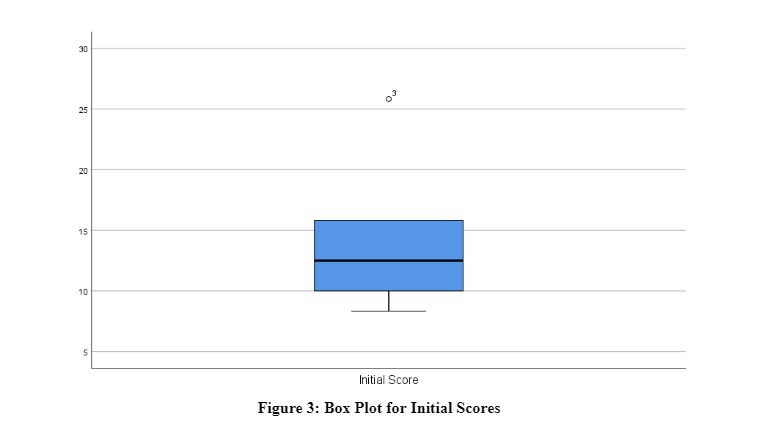
The box plot shows the minimum value, i.e. 8.33, and the maximum value, i.e. 15.83. However, there is a presence of an outlier in the data, denoted by a small dot superscripted with a 3. This indicates that the score at the third number is the outlier in the data, i.e. 25.83. It is considered an outlier because it is at an abnormal distance from the average values in the initial score. Moreover, the box plot also indicates that most scores are more than the median. The following image shows the box plot for the final scores of the participants:
In the case of the final scores, the minimum value is 35, and the maximum value is 77.5. It is also apparent from this box plot that there are no outliers in the case of final scores. The median value for the final scores appears to be 60 in the above box plot. At the same time, most participants scored less than the median value of 60. As compared to the box plot for initial scores, it can be stated that their extent of variability is significantly less in the case of the final score.
Independent Sample T-test
When two independent groups' populations are compared to see differences or similarities, an independent sample T-test is applied (Allen, Bennett, and Heritage, 2018). In the case of the data set that has been considered, the two independent groups are the control group and the trained group. The following table shows the group statistics of the model:
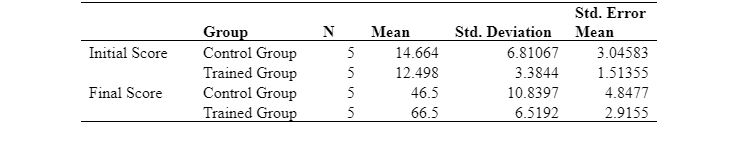
Table 3: Group Statistics
The mean values of the initial score indicate that the control group had a slightly higher score than the trained group. However, the deviation from the average value was significantly higher in the control group for the initial score. The mean values of the final score depict that the scores were improved majorly for both groups. However, the mean score of the trained group was higher, i.e. 66.5, compared to the mean value of the control group, i.e. 46.5. The deviation in the average value was again more elevated for the control group. Overall, from the group statistics, it can be evaluated that the final score has improved significantly after the intervention applied (training). However, at this stage, the significance of the difference between the mean of the two groups can be determined with the help of the following table:
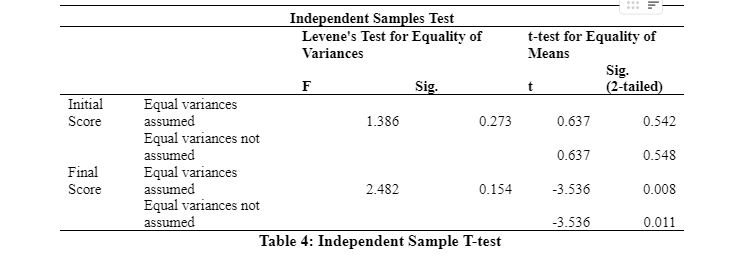
Levene's test
During data analysis using SPSS software, Leven's test is used to determine the equality of Firstly, in the above table, the sig value for Levene’s test is given, which hypothesizes that the population of variances are equal (Marshall and Boggis, 2016). In the case of the initial scores of the participants, the sig value for this test is 0.273, which is higher than the alpha value at the 95% significance level; hence the null hypothesis is accepted, stating that the population of variances is homogenous or equal. This indicates that to test the equality of means, the sig value for ‘equal variances’ will be undertaken. As per this assumption, the sig value appears to be 0.542, which means that the null hypothesis of equality of means between the control and trained groups cannot be rejected.
On the other hand, in the case of the final scores of the participants, the sig value for Levene’s test is 0.154, which is higher than the alpha value at a 95% significance level; hence the null hypothesis is accepted, stating that the population of variances are homogenous or equal. This indicates that to test the equality of means, the sig value for ‘equal variances’ will be undertaken. As per this assumption, the sig value appears to be 0.008, which means that the null hypothesis of equality of means between the control and trained groups is rejected. Henceforth, the results indicate that the final scores for the trained and control groups differ significantly.
Conclusion
The report conducted a statistical analysis and interpretation to compare quiz results between two groups: a control group and a trained group, utilizing the independent sample T-test. The intervention administered to participants involved training in virtual microscopy. Findings reveal a minor discrepancy between the initial scores of the control and trained groups. However, after training, statistically significant differences emerged in the final scores for both groups. In conclusion, the results indicate that training serves as an effective intervention in enhancing the accuracy of malaria detection through virtual microscopy.
Review the following:
References
Allen, P., Bennett, K. and Heritage, B., 2018. SPSS Statistics: A Practical Guide with Student Resource Access 12 Months. Cengage AU.
Kerr, A.W., Hall, H.K. and Kozub, S.A., 2002. Doing statistics with SPSS. Sage.
Norušis, M.J., 2011. IBM SPSS statistics 19 guide to data analysis. Upper Saddle River, New Jersey: Prentice Hall.
Park, H.M., 2015. Univariate analysis and normality test using SAS, Stata, and SPSS.
Get 3+ Free Dissertation Topics within 24 hours?


















 Download PDF File
Download PDF File








